Question

[Hoàng Như Trâm]

ChoΔDEF vuông tại D có DE=3cm, DF =4cm. Đường phân giác EI (I∈DF) cắt đường cao DK (K∈EF) tại O

a) Cm ΔKED∼ΔDEF

b) Cm \(DE^2=KE.EF\)

           \(DK^2=EK.KF\)

            \(\frac{1}{DK^2}=\frac{1}{DE^2}+\frac{1}{DF^2}\)

c) Tính DK, DI, IF

d) \(\frac{DI}{IF}=\frac{OK}{OD}\)

Answer 1

[Uyên Bùi]

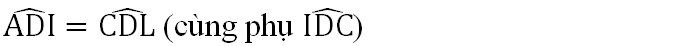
D E F I K O

a) Xét \(\Delta vuôngKEDva\Delta vuôngDEF\) có:

\(\widehat{E:}chung\)

\(\Rightarrow\Delta KED\) đồng dạng \(\Delta DEF\)

b) Vì \(\Delta KED\) đồng dạng \(\Delta DEF\) (1)

\(\Rightarrow\frac{KE}{DE}=\frac{DE}{EF}\Rightarrow DE.DE=KE.EF\Rightarrow DE^2=KE.EF\)

b₂) Xét \(\Delta VuôngKFD\) và \(\Delta vuôngDEF\)có :

\(\widehat{F:}chung\)

\(\Rightarrow\Delta KFD\) đồng dạng \(\Delta DEF\) (2)

từ (1) và (2) suy ra \(\Delta KED\) đồng dạng \(\Delta KFD\) 

\(\Rightarrow\frac{EK}{DK}=\frac{DK}{KF}\Rightarrow DK.DK=KE.KF\Rightarrow DK^2=KE.KF\)

b₃) xin lỗi mình chưa bt cách làm

c) \(\Delta DEF\) là tam giác vuông nên:

\(EF^2=DE^2.DF^2\)

\(EF=\sqrt{DE^2.DF^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)

Vì EI là đường phân giác của\(\Delta DEF\)

\(\Rightarrow\) \(\frac{DI}{DE}=\frac{IF}{EF}\Rightarrow DI=\frac{DE.IF}{EF}=\frac{3.4}{5}=2,4\left(cm\right)\)

DF=ID+IF\(\Rightarrow IF=DF-DI=4-2,4=1,6\left(cm\right)\)

Vì \(\Delta KED\) đồng dạng \(\Delta DEF\) nên:

\(\frac{DK}{DF}=\frac{DE}{EF}\Rightarrow DK=\frac{DF.DE}{EF}=\frac{4.3}{5}=2,4\left(cm\right)\)

d) Ta có \(DE^2=KE.EF\)

suy ra \(\frac{DE}{KE}=\frac{EF}{DE}\) (4)

Mà \(\frac{DE}{KE}=\frac{OK}{OD}\)( EO là đường phân giác của \(\Delta KED\)) (5)

Lại có \(\frac{EF}{DE}=\frac{IF}{DI}Hay\frac{DE}{EF}=\frac{DI}{IF}\)( EI là đường phân giác của \(\Delta DEF\)) (6)

Từ (4),(5),(6) suy ra \(\frac{DI}{IF}=\frac{OK}{OD}\)