Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn :\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\Rightarrow\frac{xy+yz+zx}{xyz}=0\Rightarrow xy+yz+zx=0\)
Thay vào:\(x^2+2yz=x^2+yz+yz=x^2+yz-xy-zx=x\left(x-y\right)-z\left(x-y\right)=\left(x-y\right)\left(x-z\right)\)
Tương tự thay vào mà quy đồng

cần c/m : nếu x+y+z=0 thì x3+y3+z3=3xyz
rồi áp dụng vô tính K=[xyz(1/x3+1/y3+1/z3)-2]2017=(3-2)2017=1

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
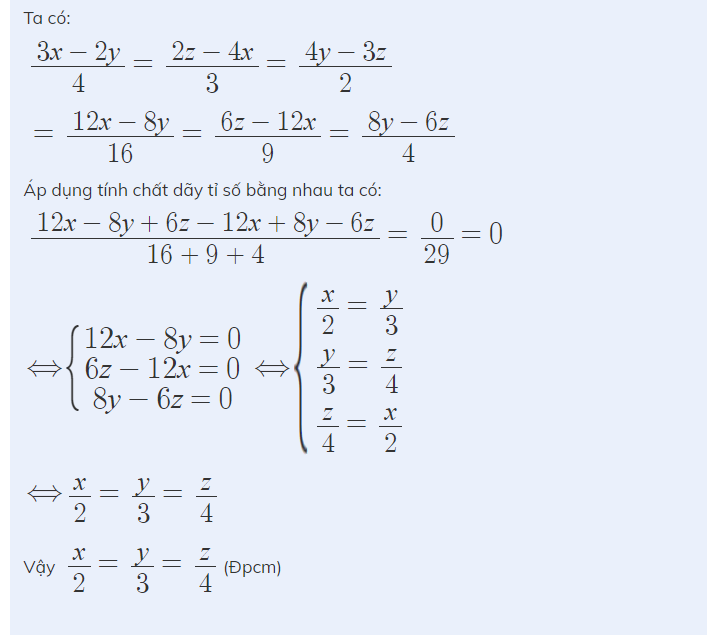

\(\frac{x^2-yz}{yz}+1+\frac{y^2-zx}{zx}+1+\frac{z^2-xy}{xy}+1=3\Leftrightarrow\frac{x^2}{yz}+\frac{y^2}{zx}+\frac{z^2}{xy}=3\)
\(\Leftrightarrow\frac{1}{xyz}\left(x^3+y^3+z^3\right)=3\Leftrightarrow x^3+y^3+z^3-3xyz=0\)
\(\Leftrightarrow\left(x+y+z\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+y+z=0\\x=y=z\end{cases}}\)
Tới đây bạn thay vào nhé :)

Câu hỏi của Vũ Thảo Vy - Toán lớp 8 - Học toán với OnlineMath.
Em xem bài ở link này nhé :)

1)\(A=\frac{b\left(2a\left(a+5b\right)+\left(a+5b\right)\right)}{a-3b}.\frac{a\left(a-3b\right)}{ab\left(a+5b\right)}=\frac{b\left(a+5b\right)\left(2a+1\right).a\left(a-3b\right)}{\left(a-3b\right).ab\left(a+5b\right)}\)
\(A=2a+1\)=>lẻ với mọi a thuộc z=> dpcm
2) từ: x+y+z=1=> xy+z=xy+1-x-y=x(y-1)-(y-1)=(y-1)(x-1)
tường tự: ta có tử của Q=(x-1)^2.(y-1)^2.(z-1)^2=[(x-1)(y-1)(z-1)]^2=[-(z+y).-(x+y).-(x+y)]^2=Mẫu=> Q=1
3) kiểm tra lại xem đề đã chuẩn chưa
hơi dài mà lười nên mình nói cách làm nha :P
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\Rightarrow xy+yz+xz=0\)
bạn cm \(\frac{1}{x^2+2yz}+\frac{1}{y^2+2xz}+\frac{1}{z^2+2xy}=0\)
tách: \(x^2+2yz=x^2+yz-xy-xz=\left(x-z\right).\left(x-y\right)\), mấy cái khác tương tự
quy đồng rồi tính ra = 0 là được