Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

HD: áp dụng BĐT Cô-si cho 3 số hạng trên, khi đó trong căn sẽ triệt tiêu các tổng suy ra đpcm

\(VT\ge3\sqrt[3]{\dfrac{x^3y^3z^3\left(x+y\right)\left(y+z\right)\left(z+x\right)}{\left(x+y\right)\left(y+z\right)\left(z+x\right)}}=3xyz\) (dpcm)

Vì \(x\ge1\Rightarrow x^2\ge x\)
Từ đó: \(P\ge\frac{x}{\left(x+y\right)^2+x}+\frac{x}{z^2+x}=x\left[\frac{1}{\left(x+y\right)^2+x}+\frac{1}{z^2+x}\right]\)
\(\ge x\cdot\frac{4}{\left(x+y\right)^2+x+z^2+x}=\frac{4x}{\left(x+y\right)^2+z^2+2x}\) (Cauchy Schwarz)
Lại có: \(\left(x+y\right)^2+z^2=x^2+y^2+z^2+2xy=3\left(x+y+z\right)\)
\(\le3\sqrt{2\left[\left(x+y\right)^2+z^2\right]}\)
\(\Rightarrow\left(x+y\right)^2+z^2\le18\)
\(\Rightarrow P\ge\frac{4x}{18+2x}=2-\frac{18}{x+9}\ge2-\frac{18}{1+9}=\frac{1}{5}\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}x=1\\y=2\\z=3\end{cases}}\)
Vậy Min(P) = 1/5 khi x = 1 ; y = 2 ; z = 3

a) Cách 1: y' = (9 -2x)'(2x3- 9x2 +1) +(9 -2x)(2x3- 9x2 +1)' = -2(2x3- 9x2 +1) +(9 -2x)(6x2 -18x) = -16x3 +108x2 -162x -2.
Cách 2: y = -4x4 +36x3 -81x2 -2x +9, do đó
y' = -16x3 +108x2 -162x -2.
b) y' = .(7x -3) +
(7x -3)'=
(7x -3) +7
.
c) y' = (x -2)'√(x2 +1) + (x -2)(√x2 +1)' = √(x2 +1) + (x -2) = √(x2 +1) + (x -2)
= √(x2 +1) +
=
.
d) y' = 2tanx.(tanx)' - (x2)' =
.
e) y' = sin
=
sin
.

Áp dụng BĐT Bunhiacôpxki:
\(1=\left(\sqrt{xy}+\sqrt{yz}+\sqrt{zx}\right)^2\le\left(x+y+z\right)\left(x+y+z\right)\)
\(\Rightarrow x+y+z\ge1\)
\(T=\frac{x^2}{x+y}+\frac{y^2}{y+z}+\frac{z^2}{z+x}\ge\frac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\frac{x+y+z}{2}\ge\frac{1}{2}\)
\(\Rightarrow T_{min}=\frac{1}{2}\) khi \(x=y=z=\frac{1}{3}\)
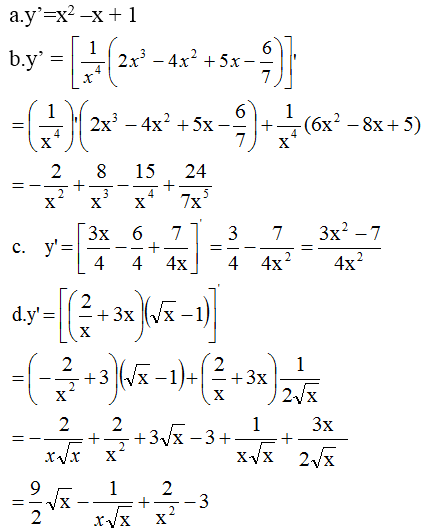
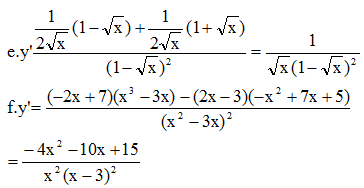
Đề bài sai, biểu thức này ko có min
vậy nó có max không thầy, nếu có thầy có thể giúp em tìm max ạ