NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HL
18 tháng 9 2017
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\sqrt{3}\)
\(\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2=3\)
\(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2}{xy}+\dfrac{2}{yz}+\dfrac{2}{xz}=3\)
\(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+2.\left(\dfrac{1}{xy}+\dfrac{1}{yz}+\dfrac{1}{xz}\right)=3\)
\(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+2.\left(\dfrac{x+y+z}{xyz}\right)=3\)
\(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+2.1=3\) ( Do x+y+z=xyz )
\(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}=3-2=1\)
Vậy P = 1
21 tháng 1 2018
Ai lm giúp mk vs câu nào cũng được. Ai làm xong sớm nhất sẽ được tick
5 tháng 5 2018
nhầm mk giải lại
vì x;y;z là 3 số dương \(\Rightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}>=\frac{9}{x+y+z}\)(bđt cauchy schwarz dạng engel)
dấu = xảy ra khi x=y=z=2
mà x+y+z<=6\(\Rightarrow\frac{9}{x+y+z}>=\frac{9}{6}=\frac{3}{2}\)\(\Rightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}.=\frac{3}{2}\)
5 tháng 5 2018
vì x;y;z là 3 số dương \(\Rightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}>=\frac{9}{x+y+z}=\frac{9}{6}=\frac{3}{2}\)(bđt caucht schwarz dạng engel)
dấu = xảy ra khi \(x=y=z=\frac{6}{3}=2\)
vậy \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}>=\frac{3}{2}\)
AH
Akai Haruma
Giáo viên
8 tháng 8 2017
Bài 3:
a) Áp dụng BĐT Cauchy-Schwarz:
\(\frac{1}{xy}+\frac{2}{x^2+y^2}=2\left(\frac{1}{2xy}+\frac{1}{x^2+y^2}\right)\) \(\geq 2.\frac{(1+1)^2}{2xy+x^2+y^2}=\frac{8}{(x+y)^2}=8\)
Dấu bằng xảy ra khi \(x=y=\frac{1}{2}\)
b) Áp dụng BĐT Cauchy-Schwarz:
\(\frac{1}{xy}+\frac{1}{x^2+y^2}=\frac{1}{2xy}+\left (\frac{1}{2xy}+\frac{1}{x^2+y^2}\right)\geq \frac{1}{2xy}+\frac{(1+1)^2}{2xy+x^2+y^2}\)
\(=\frac{1}{2xy}+\frac{4}{(x+y)^2}\)
Theo BĐT AM-GM:
\(xy\leq \frac{(x+y)^2}{4}=\frac{1}{4}\Rightarrow \frac{1}{2xy}\geq 2\)
Do đó \(\frac{1}{xy}+\frac{1}{x^2+y^2}\geq 2+4=6\)
Dấu bằng xảy ra khi \(x=y=\frac{1}{2}\)
AH
Akai Haruma
Giáo viên
8 tháng 8 2017
Bài 1: Thiếu đề.
Bài 2: Sai đề, thử với \(x=\frac{1}{6}\)
Bài 4 a) Sai đề với \(x<0\)
b) Áp dụng BĐT AM-GM:
\(x^4-x+\frac{1}{2}=\left (x^4+\frac{1}{4}\right)-x+\frac{1}{4}\geq x^2-x+\frac{1}{4}=(x-\frac{1}{2})^2\geq 0\)
Dấu bằng xảy ra khi \(\left\{\begin{matrix} x^4=\frac{1}{4}\\ x=\frac{1}{2}\end{matrix}\right.\) (vô lý)
Do đó dấu bằng không xảy ra , nên \(x^4-x+\frac{1}{2}>0\)
Bài 6: Áp dụng BĐT AM-GM cho $6$ số:
\(a^2+b^2+c^2+d^2+ab+cd\geq 6\sqrt[6]{a^3b^3c^3d^3}=6\)
Do đó ta có đpcm
Dấu bằng xảy ra khi \(a=b=c=d=1\)
10 tháng 8 2017
5) a) Đặt b+c-a=x;a+c-b=y;a+b-c=z thì 2a=y+z;2b=x+z;2c=x+y
Ta có:
\(\dfrac{2a}{b+c-a}+\dfrac{2b}{a+c-b}+\dfrac{2c}{a+b-c}=\dfrac{y+z}{x}+\dfrac{x+z}{y}+\dfrac{x+y}{z}=\left(\dfrac{x}{y}+\dfrac{y}{x}\right)+\left(\dfrac{z}{x}+\dfrac{x}{z}\right)+\left(\dfrac{z}{y}+\dfrac{y}{z}\right)\ge6\)
Vậy ta suy ra đpcm
b) Ta có: a+b>c;b+c>a;a+c>b
Xét: \(\dfrac{1}{a+c}+\dfrac{1}{b+c}>\dfrac{1}{a+b+c}+\dfrac{1}{b+c+a}=\dfrac{2}{a+b+c}>\dfrac{2}{a+b+a+b}=\dfrac{1}{a+b}\)
.Tương tự:
\(\dfrac{1}{a+b}+\dfrac{1}{a+c}>\dfrac{1}{b+c};\dfrac{1}{a+b}+\dfrac{1}{b+c}>\dfrac{1}{a+c}\)
Vậy ta có đpcm
10 tháng 8 2017
6) Ta có:
\(a^2+b^2+c^2+d^2+ab+cd\ge2ab+2cd+ab+cd=3\left(ab+cd\right)\)
\(ab+cd=ab+\dfrac{1}{ab}\ge2\)
Suy ra đpcm
B1
24 tháng 8 2017
Muốn viết tất cả các số tự nhiên từ 100 đến 999 phải dùng hết bao nhiên chữ số 5?
giải
ta có 100 chia hết cho 5
và số lớn nhất chia hết cho 5 trong dãy số này là:
995
vì cứ mỗi số chia hết cho 5 thì cách 5 đơn vị thì lại là một số chia hết cho 5
nên
từ 100-995 có số chữ số 5 là:
(995-100):5+1=180(số)
đáp số:180 số
đúng thì thanks mình nhé!
7 tháng 1 2017
x < y < z => 1/x > 1/y > 1/z
=> 3/x > 1/x + 1/y + 1/z
=> 3/x > 1/3 = 3/9
=> x < 9 (1)
Có: 1/x < 1/3 do 1/x + 1/y + 1/z = 1/3
=> x > 3 (2)
Từ (1) và (2) do x nguyên dương lẻ => x = 5 hoặc x = 7
+ Với x = 5 => 1/y + 1/z = 1/3 - 1/5 = 2/15
Có: 2/y > 1/y + 1/z
=> 2/y > 2/15
=> y < 15 (3)
Có: 2/y < 2.2/15 do 1/y + 1/z = 2/15
=> 4/2y < 4/15 => 2y > 15 => y > 15/2 (4)
Từ (3) và (4), do y nguyên dương lẻ nê y = 9 hoặc y = 11 hoặc y = 13
Giá trị tương ứng của z là: 45; 165/7; 195/11
Dễ thấy z = 45 thỏa mãn x < y < z và z nguyên dương lẻ
+ Với x = 7 => 1/y + 1/z = 1/3 - 1/7 = 4/21
Có: 2/y > 1/y + 1/z
=> 4/y > 4/21
=> y < 21 (5)
Lại có: 1/y < 4/21 do 1/y + 1/z = 4/21
=> 4/4y < 4/21 => 4y > 21 => y > 21/4 (6)
Từ (5) và (6) do y nguyên dương lẻ => y thuộc {7;9;11;13;15;17;19}
Thử từng giá trị của y ta đều thấy vô lý
Vậy x = 5; y = 9; z = 45
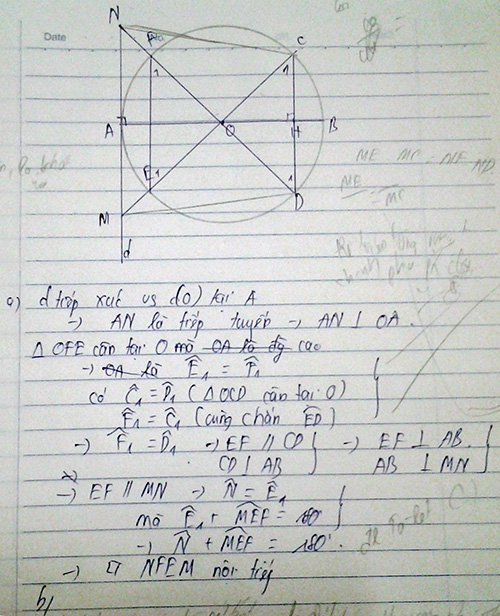
tìm trc khi hỏi
[Toán 9] Phương trình vô tỉ - Bất đẳng thức - Số nguyên tố | Diễn đàn HOCMAI - Cộng đồng học tập lớn nhất Việt Nam
Cho các số thực x,y,z thỏa mãn: Chứng minh rằng: - K2PI – TOÁN THPT | Chia sẻ Tài liệu, đề thi, hỗ trợ giải toán
CM: $x^2+y^4+z^6\leqslant 2$ - Bất đẳng thức và cực trị - Diễn đàn Toán học
Chứng minh rằng: $ x^2+y^4+z^6 \le 2 $ - Bất đẳng thức và cực trị - Diễn đàn Toán học