Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ giả thiết \(x+y+z=xyz\Leftrightarrow\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}=1\)
Khi đó \(\frac{x}{1+x^2}=\frac{\frac{1}{x}}{\frac{1}{x^2}+1}=\frac{\frac{1}{x}}{\left(\frac{1}{x}+\frac{1}{y}\right)\left(\frac{1}{x}+\frac{1}{z}\right)}=\frac{xyz}{\left(x+y\right)\left(x+z\right)}\)
Tương tự cho 2 cái còn lại ta có: \(\frac{y}{1+y^2}=\frac{xyz}{\left(y+x\right)\left(y+z\right)}\)
\(\frac{z}{1+z^2}=\frac{xyz}{\left(z+x\right)\left(z+y\right)}\)
Suy ra \(VT=\frac{xyz\left(y+z\right)+2xyz\left(z+x\right)+3xyz\left(x+y\right)}{\left(x+y\right)\left(y+z\right)\left(z+x\right)}=\frac{xyz\left(5x+4y+3z\right)}{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\)
Đpcm

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
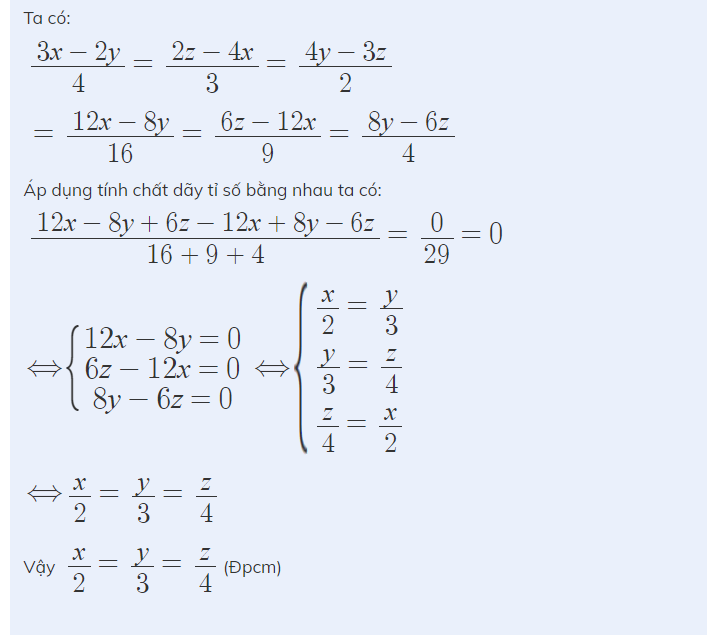

We have:
\(A=\Sigma_{cyc}\frac{1}{3xy+3zx+x+y+z}\le\frac{1}{3xy+3zx+3\sqrt[3]{xyz}}=\Sigma_{cyc}\frac{1}{3xy+3zx+3}=\Sigma_{cyc}\frac{1}{3\left(xy+zx+1\right)}\)
Dat \(\left(\frac{1}{x};\frac{1}{y};\frac{1}{z}\right)=\left(a;b;c\right)\Rightarrow abc=1\)
\(\Rightarrow A\le\Sigma_{cyc}\frac{1}{3\left(\frac{1}{ab}+\frac{1}{ca}+1\right)}=\Sigma_{cyc}\frac{a}{3\left(a+b+c\right)}=\frac{1}{3}\)
Dau '=' xay ra khi \(x=y=z=1\)

Trả lời
Từ giả thiết x+y+z=xyz <=> 1/xy + 1/yz + 1/zx = 1
Khi đó: x/1+x2 = \(\frac{1}{\frac{x}{\left(\frac{1}{z}+\frac{1}{y}\right)\left(\frac{1}{x}+\frac{1}{z}\right)}}\)\(=\frac{xyz}{\left(x+y\right)\left(x+z\right)}\)
Tương tự cho 2 cái còn lại ta có:\(\frac{y}{1+y^2}=\frac{xyz}{\left(y+x\right)\left(y+z\right)}\)
\(\frac{z}{1+z^2}=\frac{xyz}{\left(z+x\right)\left(z+y\right)}\)
Suy ra VT=\(\frac{xyz\left(y+z\right)+2xyz\left(z+x\right)+3xyz\left(x+y\right)}{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\)\(=\frac{xyz\left(5x+4y+3z\right)}{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\)
ĐPCM
Ta có:\(\frac{x}{1+x^2}=\frac{xyz}{yz+x^2yz}=\frac{xyz}{yz+x\left(xyz\right)}=\frac{xyz}{yz+x\left(x+y+z\right)}=\frac{xyz}{yz+x^2+xy+xz}=\frac{xyz}{y\left(x+z\right)+x\left(x+z\right)}\)
\(=\frac{xyz}{\left(x+z\right)\left(y+x\right)}\)
Chứng minh tương tự : \(\frac{2y}{1+y^2}=\frac{2xyz}{\left(y+z\right)\left(y+x\right)}\)
\(\frac{3z}{1+z^2}=\frac{3xyz}{\left(x+z\right)\left(x+y\right)}\)
Khi đó VT \(=\frac{xyz}{\left(x+z\right)\left(y+x\right)}+\frac{2xyz}{\left(y+z\right)\left(y+x\right)}+\frac{3xyz}{\left(x+z\right)\left(z+y\right)}\)
\(=\frac{xyz\left[y+z+2\left(z+x\right)+3\left(x+y\right)\right]}{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\)
\(=\frac{xyz\left(5x+4y+3z\right)}{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\left(đpcm\right)\)
( mình đang vội nên làm hơi tắt mong bạn thông cảm )

Nếu\(a^3+b^3+c^3=3abc\Rightarrow\orbr{\begin{cases}a+b+c=0\\a=b=c\end{cases}}\)
Thật vậy:\(a+b+c=0\Rightarrow a+b=-c\\ \Rightarrow a^3+b^3+3ab\left(a+b\right)=-c^3\Rightarrow a^3+b^3+c^3=3abc\)
Tương tự \(a=b=c\Rightarrow\orbr{\begin{cases}3abc=3a^3\\a^3+b^3+c^3=3a^3\end{cases}\Rightarrow a^3+b^3+c^3=3abc}\)
Áp dụng ta có:\(\orbr{\begin{cases}xy+yz+zx=0\\xy=yz=zx\Rightarrow x=y=z\end{cases}}\)
Khi x=y=z,ta có P=(1+1)(1+1)(1+1)=8
Khi xy+yz+zx=0,ta có:\(xy+yz=-zx\)
Tương tự:\(yz+zx=-xy\)
\(xy+zx=-yz\)
Ta có \(P=2+\frac{x+y}{z}+\frac{y+z}{x}+\frac{z+x}{y}=2+\frac{xz+yz}{z^2}+\frac{xy+xz}{x^2}+\frac{zy+xy}{y^2}\)\(=2-\left(\frac{z}{x}+\frac{x}{y}+\frac{y}{z}\right)\)\(=2-\frac{xy+yz+zx}{xyz}=2-\frac{0}{xyz}=2\)
Vậy P=8 khi x=y=z
P=2 khi xy+yz+zx=0
kho nhi