Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/

Ta có:
1-z/x=x/x-z/x=(x-z)/x(1)
1-x/y=y/y-x/y=(y-x)/y(2)
1+y/z=z/z+y/z=(y+z)/z(3)
Mà x-y-z=0( theo đề)
=>x-z=y(*)
x-y=z=>y-x=-z ( số đối) (**)
y+z=x(***)
Thay (*),(**),(***) lần lượt vào (1),(2),(3) ta đc:
A=(1-z/x)(1-x/y)(1+y/z)=(x-z)/x.(y-x)/y.(z+y)/z=y/x.(-z/y).x/z
=y.(-z).x/x.y.z=y.z.(-1).x/x.y.z=-1
Vậy A=-1

\(\frac{x-4}{y-3}=\frac{4}{3}\Rightarrow\frac{x-4}{4}=\frac{y-3}{3}\)
Áp dụng TC của DTSBN ta có:
\(\frac{x-4}{4}=\frac{y-3}{3}=\frac{x-4-y+3}{4-3}=\frac{5-1}{1}=4\)
Suy ra: (x-4)/4=4 =>x-4=16=>x=20
(y-3)/3=4=>y-3=12=>x=15
x-4/y-3=4/3
=>3.(x-4)=4.(y-3)
=>3x-12=4y-12
=>3x=4y
Mà x-y=5=>x=y+5
=>3.(y+5)=4y
=>3y+15=4y=>4y-3y=15=>y=15
Khi đó x=15+5=20
Vậy x=20;y=15

\(x+\frac{1}{y+\frac{1}{z}}=\frac{10}{7}\Leftrightarrow x+\frac{1}{y+\frac{1}{z}}=1+\frac{3}{7}\Leftrightarrow x+\frac{1}{y+\frac{1}{z}}=1+\frac{1}{\frac{7}{3}}\)
\(\Leftrightarrow x+\frac{1}{y+\frac{1}{z}}=1+\frac{1}{2+\frac{1}{3}}\Leftrightarrow x=1;y=2;z=3\)

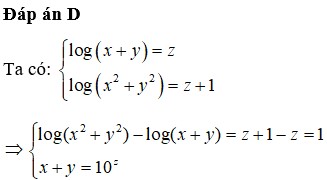
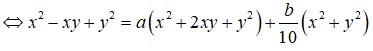
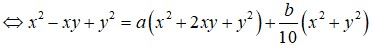
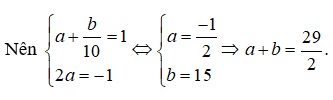
 bit lm bài này k giup tui
bit lm bài này k giup tui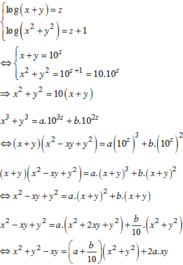
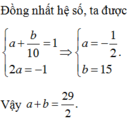


Đặt x y + z - x log x = y z + x - y log y = z x + y - z log z = 1 t
Suy ra
log x = t x y + z - z ⇔ y log x = t x y y + z - x log y = t y z + x - y ⇔ x log y = t x y z + x - y
Từ đó ta có
x log y + y log x = 2 t x y z 1 y log z + z log y = 2 t x y z 2 z log x + x log z = 2 t x y z 3
Từ (1), (2) và (3) suy ra
x log y + y log x = y log z + z log y = z log x + x log z ⇔ log x y y x = log z y y z = log z x x z ⇒ x y y x = z y y z = z x x z
Đáp án C