Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

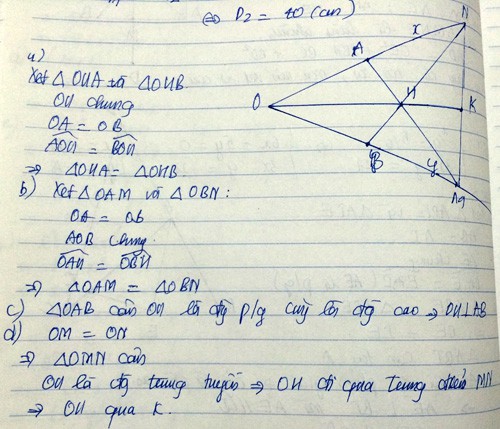
a) Xét t/g OAM và t/g OBM có:
OA = OB (gt)
AOM = BOM (gt)
OM là cạnh chung
Do đó, t/g OAM = t/g OBM (c.g.c) (đpcm)
b) Gọi K là giao điểm của AB và OM
Dễ thấy, t/g AOK = t/g BOK (c.g.c)
=> AK = BK (2 cạnh tương ứng) (1)
AKO = BKO (2 góc tương ứng)
Mà AKO + BKO = 180o ( kề bù)
Nên AKO = BKO = 90o (2)
Từ (1) và (2) => OK là đường trung trực của AB
=> đpcm
c) Có: OA = OB (gt)
AC = BD (gt)
=> OA + AC = OB + BD
=> OC = OD
Dễ thấy t/g OBC = t/g OAD (c.g.c)
=> OCB = ODA (2 góc tương ứng)
Lại có: AIC = DIB ( đối đỉnh)
Dựa vào tổng 3 góc của tam giác dễ dàng => CAI = DBI
t/g AIC = t/g BID (g.c.g) (đpcm)
d) t/g AIC = t/g BID (câu c) => IC = ID (2 cạnh tương ứng)
t/g OIC = t/g OID (c.g.c)
=> COI = DOI (2 góc tương ứng)
=> OI là phân giác COD
OM cũng là phân giác COD
=> O,I,M thẳng hàng (đpcm)

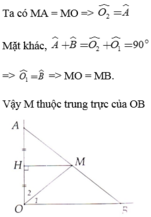
a: Xét ΔOAH và ΔOBH có
OA=OB
HA=HB
OH chung
Do đó: ΔOHA=ΔOHB
Các bạn ơi giúp mj với !