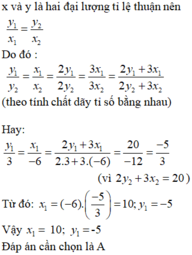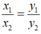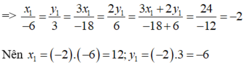Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x,y là hai đại lượng tỉ lệ thuận
=>\(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{x_1}{4}=\dfrac{y_1}{16}\)
=>\(\dfrac{x_1}{1}=\dfrac{y_1}{4}\)
mà \(3x_1+2y_1=22\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{1}=\dfrac{y_1}{4}=\dfrac{3x_1+2y_1}{3\cdot1+2\cdot4}=\dfrac{22}{11}=2\)
=>\(x_1=2\cdot1=2\)
=>Chọn D

a: x và y là hai đại lượng tỉ lệ thuận
nên \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{x_1}{2}=\dfrac{-3}{4}:\dfrac{1}{7}=-\dfrac{3}{4}\cdot7=-\dfrac{21}{4}\)
=>\(x_1=-\dfrac{21}{4}\cdot2=-\dfrac{21}{2}\)
b: \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{x_1}{-4}=\dfrac{y_1}{3}\)
mà \(y_1-x_1=-2\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{-4}=\dfrac{y_1}{3}=\dfrac{y_1-x_1}{3-\left(-4\right)}=-\dfrac{2}{7}\)
=>\(x_1=\dfrac{-2}{7}\cdot\left(-4\right)=\dfrac{8}{7};y_1=\dfrac{-2}{7}\cdot3=-\dfrac{6}{7}\)

a, Theo tính chất của tỉ lệ thuận ta có:
x1y1=x2y2=x1−34=217x1y1=x2y2=x1−34=217
⇒x1=(−34⋅2):17=−32⋅7=−212⇒x1=(−34⋅2):17=−32⋅7=−212
Vậy..............................
b, Theo t/c của tỉ lệ thuận ta có:
x1x2=y1y2x1x2=y1y2 hay x1−4=y13x1−4=y13
Áp dụng t/c của dãy tỉ số = nhau ta có:
x1−4=y13=y1−x13−(−4)=−27x1−4=y13=y1−x13−(−4)=−27
⇒⎧⎩⎨⎪⎪⎪⎪x1=−27⋅(−4)=87y1=−27⋅3=−67⇒{x1=−27⋅(−4)=87y1=−27⋅3=−67
Vậy.............
a, Theo tính chất của tỉ lệ thuận ta có:
x1y1=x2y2=x1−34=217x1y1=x2y2=x1−34=217
⇒x1=(−34⋅2):17=−32⋅7=−212⇒x1=(−34⋅2):17=−32⋅7=−212
Vậy..............................
b, Theo t/c của tỉ lệ thuận ta có:
x1x2=y1y2x1x2=y1y2 hay x1−4=y13x1−4=y13
Áp dụng t/c của dãy tỉ số = nhau ta có:
x1−4=y13=y1−x13−(−4)=−27x1−4=y13=y1−x13−(−4)=−27
⇒⎧⎩⎨⎪⎪⎪⎪x1=−27⋅(−4)=87y1=−27⋅3=−67
~Hok tốt
Câu a có cách 2 :
a) X và y là hai đại lượng tỉ lệ thuận nên ta có công thức:
X1/x2=y1/y2 do đó:
X1.y2=x2.y1
=>x1.(-2)=5.(-3)
=>x1.(-2)=-15
=>x1=-15:(-2)
=>x1=7,5
Vậy x1=7,5