Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Kết quả phép tính36.34.32 là:
A.272 B.312 C.348 D.30
2.Từ tỉ lệ thức \(\frac{a}{b}\)=\(\frac{c}{d}\)(a,b,c,d #0) ta có thể suy ra:
A.\(\frac{d}{b}\)=\(\frac{c}{a}\) B.\(\frac{a}{b}\)=\(\frac{c}{d}\)
C.\(\frac{a}{c}\)=\(\frac{d}{b}\) D.\(\frac{a}{d}\)=\(\frac{b}{c}\)
3.Nếu\(\sqrt{x}\)=4 thì x bằng:
A.\(\pm\)2 B.\(\pm\)6 C.\(\pm\)2 D.\(\pm\)16
Hok tốt!


a)Ta có:\(\Delta\)NMP cân tại N
=> ^NMP = ^NPM = 1800 − ^NMP = 1800 − ^NPM
=> ^NMA = ^NPB
Xét \(\Delta\)NMA và \(\Delta\) NPB có:
\(\hept{\begin{cases}NM=NP\left(gt\right)\\\widehat{NMA}=\widehat{NPB}\left(cmt\right)\\MA=PB\left(gt\right)\end{cases}\Rightarrow\Delta NMA=\Delta NPB\left(c.g.c\right)}\)
=> NA = NB (2 cạnh tương ứng)
=> \(\Delta\)NAB cân tại N
b)Từ \(\Delta\)NMA = \(\Delta\)NPB (cmt )
=> ^NAM = ^NBP (2 góc tương ứng) hay ^HAM = ^KBP
Xét \(\Delta\)HAM vuông tại H và \(\Delta\)KBP vuông tại K có:
\(\hept{\begin{cases}AM=BP\left(gt\right)\\\widehat{HAM}=\widehat{KBP}\left(cmt\right)\\\Delta HAM=\Delta KBP\left(ch-gn\right)\end{cases}}\)
=> HM = KP (2 cạnh tương ứng)


\(\frac{1}{2}a=\frac{2}{3}b=\frac{3}{4}c\)
\(\Leftrightarrow\)\(\frac{a}{12}=\frac{b}{9}=\frac{c}{8}\)
Ap dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{12}=\frac{b}{9}=\frac{c}{8}=\frac{a-b}{12-9}=\frac{15}{3}=5\)
suy ra \(\hept{\begin{cases}\frac{a}{12}=5\\\frac{b}{9}=5\\\frac{c}{8}=5\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}a=60\\b=45\\c=40\end{cases}}\)
Vậy.....
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{2b}{3}=\frac{3c}{4}=\frac{a}{2}=\frac{b}{\frac{3}{2}}=\frac{3c}{4}=\frac{a-b}{2-\frac{3}{2}}=\frac{15}{\frac{1}{2}}=30\)
\(\Rightarrow\)\(\hept{\begin{cases}\frac{a}{2}=30\Rightarrow a=60\\\frac{2b}{3}=30\Rightarrow b=45\\\frac{3c}{4}=30\Rightarrow c=40\end{cases}}\)

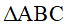 vuông tại A (AB < AC), tia phân giác của góc B cắt AC tại M. Trên tia đối của tia MB lấy điểm D sao cho MB = MD, từ điểm D vẽ đường thẳng vuông góc với AC tại N và cắt BC tại điểm E.
vuông tại A (AB < AC), tia phân giác của góc B cắt AC tại M. Trên tia đối của tia MB lấy điểm D sao cho MB = MD, từ điểm D vẽ đường thẳng vuông góc với AC tại N và cắt BC tại điểm E.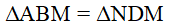 .
.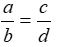 (a, b, c, d # 0) ta có thể suy ra:
(a, b, c, d # 0) ta có thể suy ra: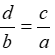 B.
B. 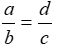
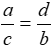 D.
D.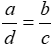
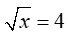 thì x bằng:
thì x bằng: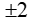 B.
B. 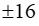 C. 2 D.16
C. 2 D.16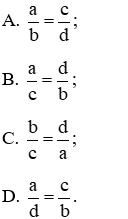
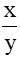
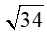 cm. D. 8cm.
cm. D. 8cm.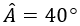 khi đó số đo của góc B bằng
khi đó số đo của góc B bằng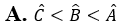
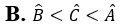
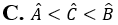
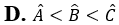
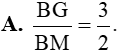
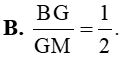
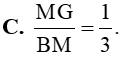
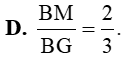
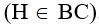 . Khẳng định nào sau đây là đúng?
. Khẳng định nào sau đây là đúng?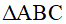 và
và 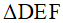 có
có 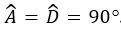 . Để kết luận
. Để kết luận 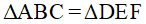 theo trường hợp cạnh huyền – cạnh góc vuông, cần có thêm điều kiện nào sau đây?
theo trường hợp cạnh huyền – cạnh góc vuông, cần có thêm điều kiện nào sau đây?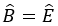
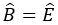
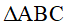 vuông tại A (AB < AC), tia phân giác của góc B cắt AC tại M. Trên tia đối của tia MB lấy điểm D sao cho MB = MD, từ điểm D vẽ đường thẳng vuông góc với AC tại N và cắt BC tại điểm E.
vuông tại A (AB < AC), tia phân giác của góc B cắt AC tại M. Trên tia đối của tia MB lấy điểm D sao cho MB = MD, từ điểm D vẽ đường thẳng vuông góc với AC tại N và cắt BC tại điểm E.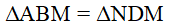 .
.
