Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

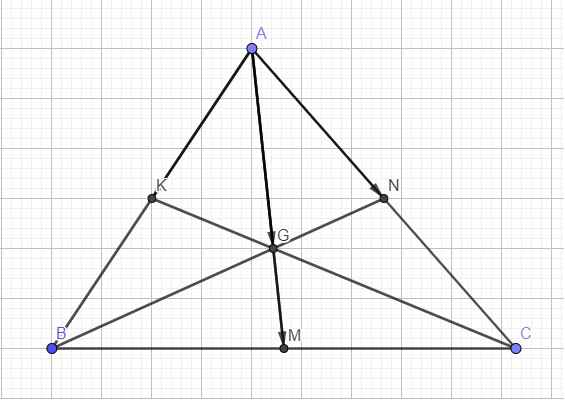
Theo tính chất trọng tâm ta có: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
Mặt khác AM là trung tuyến nên: \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\Rightarrow3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\) (1)
K là trung điểm AB, N là trung điểm AC nên: \(\left\{{}\begin{matrix}\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AB}\\\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=2\overrightarrow{AK}\\\overrightarrow{AC}=2\overrightarrow{AN}\end{matrix}\right.\) (2)
(1);(2) \(\Rightarrow3\overrightarrow{AG}=2\left(\overrightarrow{AK}+\overrightarrow{AN}\right)\)

1) Các vecto bằng vecto EF là:
\(\overrightarrow{EF}=\overrightarrow{DO}=\overrightarrow{OA}=\overrightarrow{CB}\)

Mình không biết trả lời.Mình mới học lớp 5 thôi .Mong bạn thông cảm nhé!

A B C P M N
a) \(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=\frac{1}{2}\overrightarrow{AB}+2\left(\overrightarrow{AC}-\overrightarrow{AB}\right)=2\overrightarrow{AC}-\frac{3}{2}\overrightarrow{AB}\)
Do \(\overrightarrow{NA}+2\overrightarrow{NC}=\overrightarrow{0}\)nên N thuộc đoạn AC và \(\overrightarrow{AN}=\frac{2}{3}\overrightarrow{AC}\)
\(\overrightarrow{PN}=\overrightarrow{PA}+\overrightarrow{AN}=-\frac{1}{2}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}\)
b) Ta thấy \(\overrightarrow{PN}=\frac{1}{3}\left(2\overrightarrow{AC}-\frac{3}{2}\overrightarrow{AB}\right)=\frac{1}{3}\overrightarrow{PM}\). Suy ra M,N,P thẳng hàng (đpcm).

\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}\)
\(=\overrightarrow{AC}+\overrightarrow{CA}\)
\(=\overrightarrow{0}\)

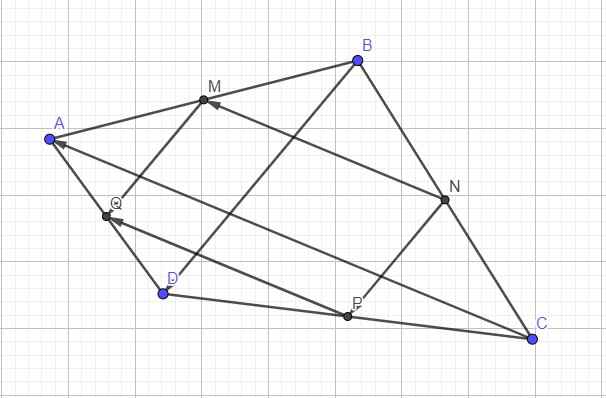
Do M là trung điểm AB, Q là trung điểm AD
\(\Rightarrow\) MQ là đường trung bình tam giác ABD
\(\Rightarrow\overrightarrow{MQ}=\dfrac{1}{2}\overrightarrow{BD}\)
Tương tự ta có NP là đường trung bình tam giác BCD
\(\Rightarrow\overrightarrow{NP}=\dfrac{1}{2}\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{NP}=\overrightarrow{MQ}\)
b. MN là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{NM}=\dfrac{1}{2}\overrightarrow{CA}\)
PQ là đường trung bình tam giác ACD
\(\Rightarrow\overrightarrow{PQ}=\dfrac{1}{2}\overrightarrow{CA}\)
\(\Rightarrow\overrightarrow{PQ}=\overrightarrow{NM}\)
\(\overrightarrow{u}+\overrightarrow{v}=\left(1+2;2-3\right)=\left(3;-1\right)\)
\(\overrightarrow{u}-\overrightarrow{v}=\left(1-2;2+3\right)=\left(-1;5\right)\)
\(2\overrightarrow{u}=\left(2;4\right)\)
\(3\overrightarrow{v}=\left(6;-9\right)\)
\(2\overrightarrow{u}+3\overrightarrow{v}=\left(2+6;4-9\right)=\left(8;-5\right)\)