Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

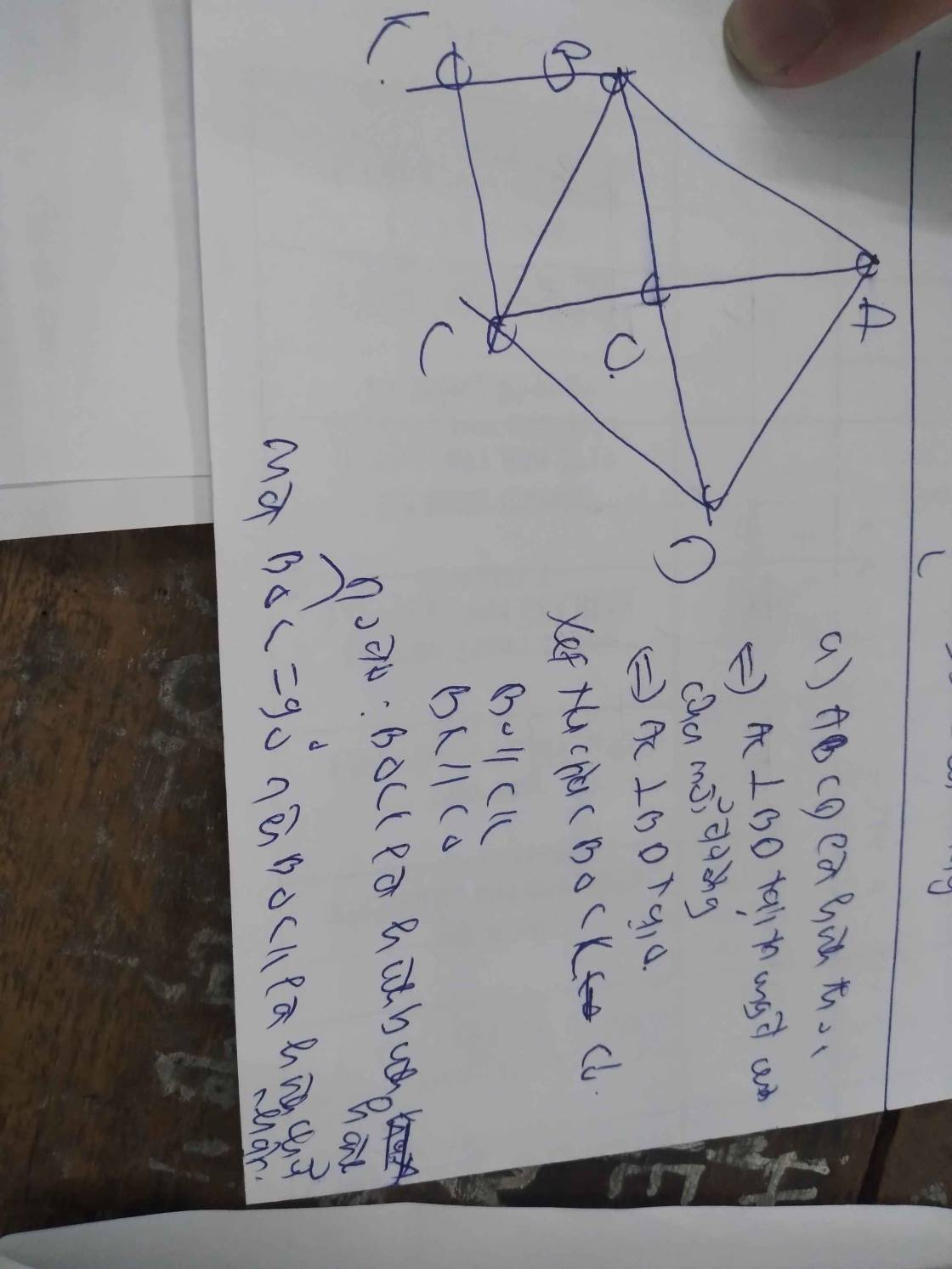
a) Tứ giác BOCK là tứ giác cân.
Để chứng minh điều này, ta cần chứng minh hai cặp góc của tứ giác BOCK bằng nhau.
Góc BOC và góc BKC là hai góc đối nhau nằm ở cùng một cạnh BC, nên chúng bằng nhau:
Góc BOC = Góc BKC. Góc BCO và góc BCK là hai góc đối nhau nằm ở cùng một cạnh BC, nên chúng bằng nhau: Góc BCO = Góc BCK.
Vì vậy, tứ giác BOCK có hai cặp góc bằng nhau, tức là tứ giác BOCK là tứ giác cân.
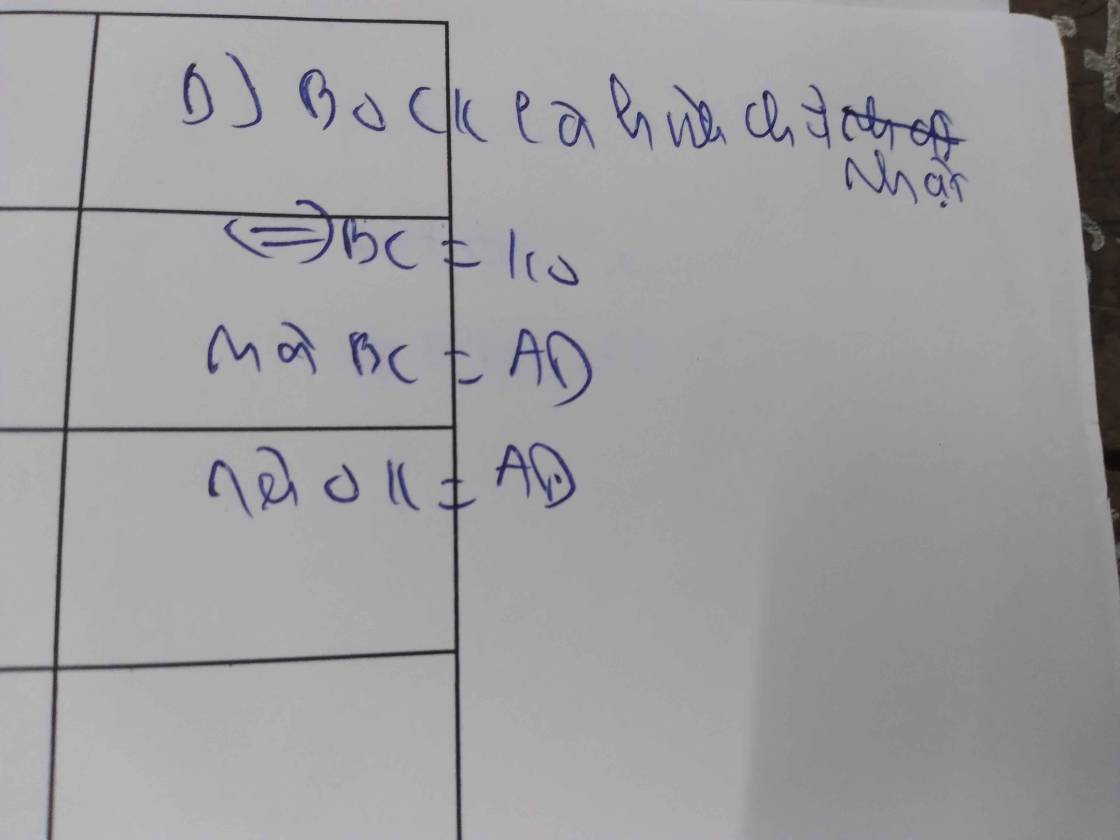
b) Ta cần chứng minh CM : OK = AD.
Vì tứ giác BOCK là tứ giác cân, nên ta có BC = BK.
Do đó, tam giác BCK là tam giác cân, nên ta có CM là đường trung tuyến của tam giác BCK.
Vì vậy, ta có CM = MK.
Từ đó, ta có CM : OK = MK : OK = 1 : 1 = 1.Tuy nhiên, để chứng minh CM : OK = AD, ta cần thêm thông tin về mối quan hệ giữa các đoạn thẳng trong hình thoi ABCD.


a) Xét tam giác \(ADC\) có \(OF//DC\), theo định lí Thales ta có:
\(\frac{{AF}}{{AD}} = \frac{{AO}}{{AC}}\) (1)
Xét tam giác \(ABC\) có \(OE//BC\), theo định lí Thales ta có:
\(\frac{{AE}}{{AB}} = \frac{{AO}}{{AC}}\) (2)
Từ (1) và (2) suy ra, \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AB}}\)
Xét tam giác \(ABD\) có:
\(\frac{{AF}}{{AD}} = \frac{{AE}}{{AB}}\)
Theo định lí Thales đảo suy ra \(EF//BD\).
b) Xét tam giác \(ADC\) có \(OH//AD\), theo định lí Thales ta có:
\(\frac{{CH}}{{CD}} = \frac{{CO}}{{AC}}\) (3)
Xét tam giác \(ABC\) có \(OG//AB\), theo định lí Thales ta có:
\(\frac{{CG}}{{BC}} = \frac{{CO}}{{AC}}\) (4)
Từ (3) và (4) suy ra, \(\frac{{CH}}{{CD}} = \frac{{CG}}{{BC}}\)
Theo định lí Thales đảo suy ra \(GH//BD\).
Xét tam giác \(BCD\) có \(GH//BD\), theo định lí Thales ta có:
\(\frac{{CH}}{{DH}} = \frac{{CG}}{{BG}} \Rightarrow CH.BG = DH.CG\) (điều phải chứng minh).
a: Xét ΔADC có OF//DC
nên AF/AD=AO/AC
Xét ΔABC có EO//BC
nên AE/AB=AO/AC
=>AF/AD=AE/AB
=>EF//BD
b: OH//AD
=>CH/CD=CO/CA
OG//AB
=>CG/BC=CO/CA
=>CG/BC=CH/CD
=>GH//BD
=>CH/DH=CG/BG
=>CH*BG=DH*CG

a: Xét tứ giác AKCI có
AK//CI
AI//CK
Do đó: AKCI là hình bình hành

Xét tam giác ABC có OE // BC . áp dụng định lý ta-lét ta có
AE/AB=AO/AC (1)
Xét tam giác ADC có OF//CD . áp dụng định lý ta-lét ta có
AF/AD=AO/AC (2)
TỪ (1)(2) suy ra AE/AB=AF/AD
Xét tam giác ABD có AE/AB=AF/AD (CMT) . áp dụng định ý ta-lét đảo ta suy ra EF//BD (đpcm)
câu b )
áp dụng định lý ta -lét cho tam giác ACD có OH//AD suy ra
CH/DH=CO/AO (3)
Aps dụng định lý ta-lét cho tam giác abc có OG//AB có
CG/GB=OC/OA (4)
TỪ (3)(4) suy ra CH/DH=CG/GB
Suy ra CH.GB=HD.CG (đpcm)

A B C D E F O G H
a) Trong tam giác ABC có OE // BC nên \(\frac{AE}{AB}=\frac{AO}{AC}\)( theo định lí Ta-let )
Trong tam giác ACD có OF // CD nên \(\frac{AF}{AD}=\frac{AO}{AC}\) ( theo định lí Ta-let )
Vậy \(\frac{AE}{AB}=\frac{AF}{AD}\Rightarrow FE//BD\)( áp dụng định lí Ta-let đảo tong tam giác ABD )
b) Tương tự trong tam giác ABC có : OG // AB nên \(\frac{CG}{BG}=\frac{CO}{OA}\)
Trong tam giác ACD có OH // AD nên \(\frac{CH}{DH}=\frac{CO}{OA}\)
Vậy \(\frac{CG}{GB}=\frac{CH}{GB}\Rightarrow CG.DH=CH.GB\)

a. Trong ΔABC có OE // BC nên : \(\frac{AE}{AB}=\frac{AO}{AC}\) (Talet)
Trong ΔACD có OF// CD nên : \(\frac{AF}{AD}=\frac{AO}{AC}\) ( Talet)
Vậy \(\frac{AE}{AB}=\frac{AF}{AD}\) => EF//BD(ap dung Ta let dao trong ΔABD)
b. Tuong tu trong ΔABC co OG//AB nen \(\frac{CG}{BG}=\frac{CO}{OA}\)
Trong ΔACD co OH // AD nen : \(\frac{CH}{DH}=\frac{CO}{OA}\)
Vay \(\frac{CG}{GB}=\frac{CH}{GB}\) => CG.DH = CH.BG
Nguồn: haybuu (hoidap247)

a. Trong ΔABC co OE // BC nen : AE/AB = AO/AC (ta let)
Trong ΔACD co OF// CD nen : AF/AD = AO/AC ( ----)
Vay AE/AB = AF/AD => FE //BD (ap dung Ta let dao trong ΔABD)
b. Tuong tu Trong ΔABC co OG//AB nen CG/BG = CO/OA
Trong ΔACD co OH // AD nen : CH/DH = CO/OA
Vậy CG/GB=CH/GB=>CG.DH=CH.BG
k mk nha