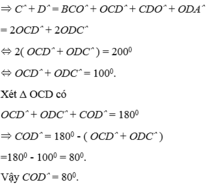Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Leftrightarrow\widehat{C}+\widehat{D}=360^o-\left(\widehat{A}+\widehat{B}\right)\)
\(\widehat{COD}=180^o-\frac{1}{2}\left(\widehat{C}+\widehat{D}\right)\)
\(=180^o-\frac{1}{2}\left[360^o-\left(\widehat{A}+\widehat{B}\right)\right]\)
\(=\frac{1}{2}\left(\widehat{A}+\widehat{B}\right)\)

ta có A+B=360-(D+C)
<=> A+B=360-2(180-ODC-OCD)=360-360+2.COD=2COD
\(\Rightarrow\widehat{COD}=\frac{\widehat{A}+\widehat{B}}{2}\)
Xét \(\Delta COD\)có :
\(\widehat{COD}=180^o-\left(\widehat{C_1}+\widehat{D_1}\right)\)
\(=180^o-\frac{\widehat{C}+\widehat{D}}{2}\)
xÉT tứ giác ABCD có :
\(\widehat{C}+\widehat{D}=360^o-\left(\widehat{A}+\widehat{B}\right)\)
Do đó : \(\widehat{COD}=180^o-\frac{360^o-\left(\widehat{A}+\widehat{B}\right)}{2}\)
\(\Rightarrow\widehat{COD}=\frac{\widehat{A}+\widehat{B}}{2}\)(đpcm)

ta có A+B=360-(D+C)
<=> A+B=360-2(180-ODC-OCD)=360-360+2.COD=2COD
=>COD=(A+B)/2

ta có A+B=360-(D+C)
<=> A+B=360-2(180-ODC-OCD)=360-360+2.COD=2COD
=>COD=(A+B)/2