Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A C B D P O M K L S T E F
Gọi E và F lần lượt là trung điểm của PA và PD.
Ta thấy: \(\Delta\)PAK vuông tại K có trung tuyến KE => KE = 1/2.AP. Mà MF là đường trung bình \(\Delta\)PAD
Nên KE = MF (=1/2AP). Tương tự: FL = ME. Ta có: ^KEM = ^MFL (= ^PFM + Sđ(BC = ^PEM + Sđ(BC )
Suy ra: \(\Delta\)KEM = \(\Delta\)MFL (c.g.c) => KM = ML (Cạnh tương ứng)
Ta thấy: ^KML = ^EMF - ^EMK - ^FML = 1800 - ^PFM - ^FLM - ^FML (^EMK = ^ FLM vì \(\Delta\)KEM = \(\Delta\)MFL)
= ^PFL = 2.^PDL = 2.^PAK => ^KML = 2.^PDL = 2.^PAK
Ta lại có: ^BDT = ^BDC - ^TDL = 1/2.^KML - (900 - ^DML) = 1/2.^KML - ^OML = ^OMK - 1/2.^KML
= ^OMK - ^PAK = ^SAK - ^PAK = ^CAS => ^BDT = ^CAS
Mặt khác: ^MTL = ^AOC = 2.^MDL (=Sđ(AC ) => \(\Delta\)MLT ~ \(\Delta\)ACO (g.g)
=> \(\frac{LT}{CO}=\frac{ML}{AC}\)=> LT. AC = ML.CO = MK.BO (Do ML = MK). Tương tự \(\Delta\)KSM ~ \(\Delta\)BOD
Từ đó; LT.AC = MK.BO = KS.BD => DT.AC = AS.DB => \(\frac{DT}{AS}=\frac{DB}{AC}\). Kết hợp với ^BDT = ^CAS (cmt)
=> \(\Delta\)CSA ~ \(\Delta\)BTD (c.g.c) => \(\frac{CS}{BT}=\frac{SA}{TD}=\frac{KS}{LT}\)=> KS.BT = CS.LT (đpcm).

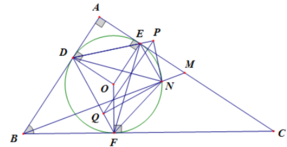
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.
Lời giải
a) Vì điểm K nằm trên đường tròn ngoại tiếp ΔBDE nên tứ giác DKBE nội tiếp đường tròn
Suy ra ˆBEK=ˆBDK𝐵𝐸𝐾^=𝐵D𝐾^ (2 góc nội tiếp cùng chắn cung BK)
Hay ˆAEK=ˆFDK𝐴𝐸𝐾^=FD𝐾^
Vì tứ giác DKFC nội tiếp đường tròn nên ˆFCK=ˆFDK𝐹𝐶𝐾^=FD𝐾^
Suy ra ˆAEK=ˆFCK𝐴𝐸𝐾^=FC𝐾^, hay ˆAEK=ˆACK𝐴𝐸𝐾^=AC𝐾^
Do đó tứ giác AKCE nội tiếp đường tròn
Suy ra ˆKAE+ˆKCE=180∘𝐾AE^+𝐾𝐶𝐸^=180∘
Mà ˆKCD+ˆKCE=180∘𝐾𝐶D^+𝐾𝐶𝐸^=180∘ (hai góc kề bù)
Do đó ˆKAE=ˆKCD𝐾AE^=𝐾𝐶D^ hay ˆKAB=ˆKCD𝐾AB^=𝐾𝐶D^
Do tứ giác BKDE nội tiếp đường tròn nên ˆKDE+ˆKBE=180∘𝐾𝐷E^+𝐾𝐵𝐸^=180∘
Mà ˆKBA+ˆKBE=180∘𝐾𝐵𝐴^+𝐾𝐵𝐸^=180∘ (hai góc kề bù)
Do đó ˆKDE=ˆKBA𝐾𝐷E^=𝐾𝐵𝐴^ hay ˆKBA=ˆKDCKBA^=𝐾𝐷𝐶^
Xét ΔDKC và ΔBKA có:
ˆKBA=ˆKDCKBA^=𝐾𝐷𝐶^ (chứng minh trên)
ˆKAB=ˆKCD𝐾AB^=𝐾𝐶D^ (chứng minh trên)
Suy ra (g.g)
Do đó KCKA=KDKB𝐾𝐶𝐾A=𝐾D𝐾𝐵
Hay KCKD=KAKB𝐾𝐶𝐾𝐷=𝐾𝐴𝐾𝐵
Ta có: ˆBKD=ˆDKC+ˆBKC𝐵𝐾D^=𝐷𝐾𝐶^+𝐵𝐾𝐶^; ˆAKC=ˆBKA+ˆBKC𝐴𝐾𝐶^=𝐵𝐾𝐴^+𝐵𝐾𝐶^
Mà ˆDKC=ˆBKA𝐷𝐾𝐶^=𝐵𝐾A^, suy ra ˆDKB=ˆCKA𝐷𝐾𝐵^=𝐶𝐾A^
Xét ΔKBD và ΔKAC có:
ˆDKB=ˆCKA𝐷𝐾𝐵^=𝐶𝐾A^ (chứng minh trên)
KCKD=KAKB𝐾𝐶𝐾𝐷=𝐾𝐴𝐾𝐵 (chứng minh trên)
Suy ra (c.g.c)
Do đó ˆKBD=ˆKAC𝐾𝐵D^=𝐾𝐴𝐶^
Hay ˆKBF=ˆKAF𝐾𝐵𝐹^=𝐾𝐴𝐹^
Suy ra tứ giác AKFB nội tiếp đường tròn
Do đó ˆBKF=ˆBAF𝐵𝐾𝐹^=BAF^ (2 góc nội tiếp chắn cung BF)
Suy ra ˆBKF=ˆBAC=ˆBDC𝐵𝐾𝐹^=𝐵𝐴𝐶^=𝐵D𝐶^ (do ˆBAC,ˆBDC𝐵𝐴𝐶^,𝐵D𝐶^ cùng chắn cung BC) (1)
Ta có: ˆBDC=ˆFDC=ˆFKC𝐵D𝐶^=𝐹D𝐶^=𝐹𝐾𝐶^ (cùng chắn cung FC) (2)
Xét ΔBMC có ˆMBC+ˆMCB+ˆBMC=180∘𝑀𝐵𝐶^+𝑀𝐶𝐵^+𝐵𝑀𝐶^=180∘ (tổng ba góc trong một tam giác)
Mà ˆMBC=ˆBAC,ˆMCB=ˆBDC𝑀𝐵𝐶^=𝐵𝐴𝐶^,𝑀𝐶𝐵^=𝐵D𝐶^(Góc tạo bởi tiếp tuyến và dây cung)
Suy ra ˆBAC+ˆBDC+ˆBMC=180∘𝐵𝐴𝐶^+𝐵𝐷𝐶^+𝐵𝑀𝐶^=180∘ (3)
Từ (1); (2) và (3) suy ra ˆBKF+ˆFKC+ˆBMC=180∘𝐵𝐾𝐹^+𝐹𝐾𝐶^+𝐵𝑀𝐶^=180∘
Hay ˆBKC+ˆBMC=180∘𝐵𝐾𝐶^+𝐵𝑀𝐶^=180∘
Do đó tứ giác BKCM nội tiếp đường tròn
b) Ta có ˆBKF=ˆBDC𝐵𝐾𝐹^=𝐵D𝐶^ (chứng minh câu a)
Suy ra ˆBKF=ˆBDE=ˆBKE𝐵𝐾𝐹^=𝐵DE^=𝐵𝐾𝐸^ (Do tứ giác DKBE nội tiếp đường tròn)
Mà 2 điểm F và E nằm cùng phía so với BK
Suy ra 3 điểm K; F; E thẳng hàng
Hay F nằm trên KE (*)
Vì ˆBKF=ˆBAC,ˆCKF=ˆBDC,ˆBAC=ˆBDC𝐵𝐾𝐹^=𝐵𝐴𝐶^,𝐶𝐾𝐹^=𝐵D𝐶^,𝐵𝐴𝐶^=𝐵D𝐶^
Nên ˆBKF=ˆCKF𝐵𝐾𝐹^=𝐶𝐾𝐹^
Suy ra ˆBKE=ˆCKE𝐵𝐾𝐸^=𝐶𝐾𝐸^ (Do K; F; E thẳng hàng)
Do đó KE là phân giác của ˆBKC𝐵𝐾𝐶^ (4)
Xét (O) có MB, MC là 2 tiếp tuyến cắt nhau tại M
Nên MB = MC
Do đó tam giác MBC cân tại M
Suy ra ˆMBC=ˆMCB𝑀𝐵𝐶^=𝑀𝐶𝐵^
Xét tứ giác BKCM nội tiếp đường tròn có ˆMBC=ˆMKC,ˆMCB=ˆMKB𝑀𝐵𝐶^=𝑀𝐾𝐶^,𝑀𝐶𝐵^=𝑀𝐾𝐵^
Suy ra ˆMKC=ˆMKB𝑀𝐾𝐶^=𝑀𝐾𝐵^
Do đó KM là phân giác của ˆBKC𝐵𝐾𝐶^ (5)
Từ (4) và (5) suy ra 3 điểm K; M; E thẳng hàng hay M nằm trên KE (**)
Từ (*) và (**) suy ra 3 điểm E; M; F thẳng hàng
Vậy 3 điểm E; M; F thẳng hàng.