Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ: A B C D E F I
a) Xét \(\Delta ADC\) có:
AE = ED (gt)
AI = IC (gt)
=> EI là đường trung bình
=> EI // DC
Xét \(\Delta CAB\) có:
AI = IC (gt)
BF = FC (gt)
=> IF là đường trung bình
=> IF // AB
b) Ta có: EF \(\le\) EI + IF
mà IF + EF = \(\dfrac{1}{2}\) AB + \(\dfrac{1}{2}\) CD
= \(\dfrac{1}{2}\) (AB + CD)
=> EF \(\le\) \(\dfrac{\left(AB+CD\right)}{2}\) (đpcm)

a: Xét ΔDAB có
I là trung điểm của BD
E là trung điểm của AD
DO đó: IE là đường trung bình
=>IE//AB
Xét ΔBDC có
I là trung điểm của BD
F là trung điểm của BC
Do đó: IF là đường trung bình
=>IF//DC
b: \(\dfrac{AB+CD}{2}=EI+FI>=EF\)

EF là đg trung bình ứng cạnh DC của tam giác ADC => EF= CD/2 tất nhiên < (AB+CD)/2

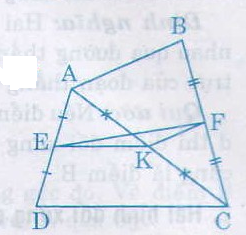
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2 = (AB+CD)/2
Vậy EF ≤ (AB+CD)/2
27. Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh các độ dài EK và CD, KF và AB.
b) Chứng minh rằng EF \(\le\dfrac{AB+CD}{2}\)
Bài giải:

a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK =\(\dfrac{CD}{2}\)
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = \(\dfrac{AB}{2}\)
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = \(\dfrac{CD}{2}\) + \(\dfrac{AB}{2}\) = \(\dfrac{\left(AB+CD\right)}{2}\)
Vậy EF ≤ \(\dfrac{\left(AB+CD\right)}{2}\)

Bạn ơi hình như câu a bạn ghi đề sai phải là EF bé hơn bằng (AB+CD)/2 chứ
Cho mình hỏi cái dấu đó ko phải dấu bé hơn hoặc bằng sao ??

Áp dụng định lý 2 của đường trung bình trong hình thang
Có AB//CD => ABCD là hình thang. EF là đường trung bình của hình thang
Nên \(\text{EF}=\frac{CD+AB}{2}\) .
Sai rồi vì EF đâu phải đường trung bình đâu, E là trung điểm BD, F là trung điểm AC và đề bài yêu cầu chứng minh EF=(CD-AB)/2 mà.

a: Xét ΔADC có
E là trung điểm của AD
I là trung điểm của AC
Do đó: EI là đường trung bình
=>EI=DC/2 và EI//DC
Xét ΔCAB có
I là trung điểm của CA
F là trung điểm của CB
Do đó: IF là đường trung bình
=>IF//AB và IF=AB/2
b: EF<=EI+FI=(AB+CD)/2
c: Để EF=(AB+CD)/2 thì E,I,F thẳng hàng
=>AB//CD