Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
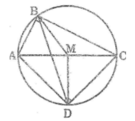
Gọi M là trung điểm của AC
Tam giác ABC vuông tại B có BM là đường trung tuyến nên:
BM = (1/2).AC (tính chất tam giác vuông)
Tam giác ACD vuông tại D có DM là đường trung tuyến nên:
DM = (1/2).AC (tính chất tam giác vuông)
Suy ra: MA = MB = MC = MD
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn tâm M bán kính bằng (1/2).AC.
Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc 1 đường tròn
Tâm là trung điểm của BD
Bán kính là một nửa của BD
a) Theo giả thiết, =
=
.60o = 30o
=
+
(tia CB nằm giữa hai tia CA, CD)
=> = 60o + 30o = 90o (1)
Do DB = CD nên ∆BDC cân => =
= 30o
Từ đó = 60o + 30o = 90o (2)
Từ (1) và (2) có +
= 180o nên tứ giác ABDC nội tiếp được.
b) Vì = 90o nên AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC, do đó tâm đường tròn ngoại tiếp tứ giác ABDC là trung điểm AD.
a: Xét tứ giác ABCD có
\(\widehat{B}+\widehat{D}=180^0\)
nên ABCD là tứ giác nội tiếp
DC = DA
OA = OC
Do đó OD là trung trực của đoạn thẳng AC : suy ra OD vuông góc với AC
Tứ giác OECH có góc CEO + góc CHO = 180 độ
Suy ra tứ giác OECH là tứ giác nội tiếp
Bạn kham khảo tại link:
Câu hỏi của Trần Thị Thảo Ngọc - Toán lớp 9 - Học toán với OnlineMath
https://www.google.com.vn/url?sa=t&rct=j&q=&esrc=s&source=web&cd=8&cad=rja&uact=8&ved=2ahUKEwiz7t_v7vXcAhWadn0KHXIyAMcQFjAHegQIAxAB&url=https%3A%2F%2Folm.vn%2Fhoi-dap%2Fquestion%2F1014815.html&usg=AOvVaw0h6fXqwysaNQwyYWr3DvPL
Hãy xác định hàm số y=ax+b, biết: đồ thị hàm số song song với đường thẳng y=2x và cắt trục hoành tại điểm có hoành độ bằng -3
/
Gọi E là trung điểm của AC
∆ACD vuông tại D
DE là đường trung tuyến của ∆ACD
⇒ DE = AE = CE = AC : 2 (1)
∆ABC vuông tại B
BE là đường trung tuyến của ∆ABC
⇒ BE = AE = CE = AC : 2 (2)
Từ (1) và (2) ⇒ AE = BE = CE = DE
Vậy A, B, C, D cùng nằm trên đường tròn tâm E, bán kính AE