Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

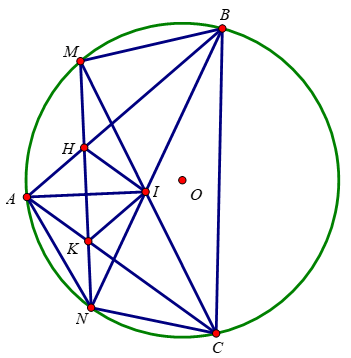
a) Xét tứ giác HMBI có:
∠HMI = ∠HBI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AN}=\widebat{CN}\))
Mà 2 góc này cùng nhìn cạnh HI
=> Tứ giác BMHI nội tiếp
b) Xét ΔMNI và ΔMKC có:
∠KMC là góc chung
∠MNI = ∠KCM (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{BM}\))
=> ΔMNI ∼ ΔMCK => \(\frac{MN}{MC}=\frac{MI}{MK}\) => MN.MK = MC.MI
c) Xét tứ giác NKIC có:
∠KNI = ∠KCI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{MB}\))
Mà 2 góc này cùng nhìn cạnh KI
=> Tứ giác NKIC là tứ giác nội tiếp
=> ∠NKI + ∠NCI = 180o (1)
Xét đường tròn (O) có:
\(\hept{\begin{cases}\widehat{ANK}=\widehat{ACM}\left(\text{2 góc nội tiếp cùng chắn cung AM}\right)\\\widehat{NAK}=\widehat{NCA}\left(\text{2 góc nội tiếp cùng chắn 2 cung BẰNG NHAU}\widebat{AN}=\widebat{CN}\right)\end{cases}}\)
=> ∠ANK + ∠NAK = ∠ACM + ∠NCA = ∠NCI (2)
Xét tam giác AKN có: ∠ANK + ∠NAK + ∠NKA = 180o (3)
Từ (1), (2), (3) => ∠NKI = ∠NKA
Xét tam giác IKN và tam giác AKN có:
∠NKI = ∠NKA
KN là cạnh chung
∠KNI = ∠KNA (2 góc nội tiếp chắn 2 cung bằng nhau)
=> ΔIKN = ΔAKN
=> IK=AK =>ΔAKI cân tại K
Tứ giác NKIC là tứ giác nội tiếp
Mặt khác ∠KCN = ∠ABN (2 góc nội tiếp cùng chắn cung AN của (O))
∠BAC = ∠BNC (2 góc nội tiếp cùng chắc cung BC của (O))
=> Tứ giác AHIK là hình bình hành
Mà IK = AK
=> Tứ giác AHIK là hình thoi.
CÒN LẠI TỰ LÀM LÀM NHA


Ta có tam giác EPQ cân tại E và CQ là phân giác góc BCA, nên E P Q ^ = E Q P ^ = H Q C ^ = 90 0 − H C Q ^ = 90 0 − P C K ^ .
Do đó E P Q ^ + P C K ^ = 90 0 , nên P K ⊥ A C .

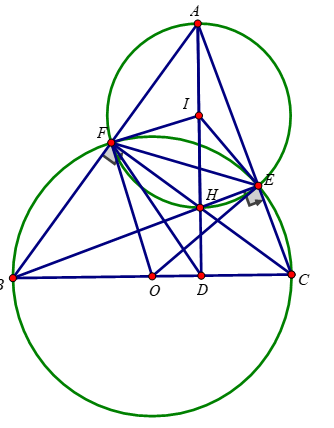
a: Xét (O) có
góc BEC, góc BDC đều là các góc nội tiếp chắn nửa đường tròn
=>góc BEC=góc BDC=90 độ
=>CE vuông góc AB, BD vuông góc AC
Xét ΔABC có
CE,BD là đường cao
CE cắt BD tại H
=>H là trực tâm
=>AH vuông góc BC tại F
góc BEH+góc BFH=180 độ
=>BEHF nội tiếp
b: Xét ΔHCB có CO/CB=CM/CH
nên OM//BH
=>góc COM=góc CBH
=>góc COM=góc FEC
=>góc MOF+góc FEM=180 độ
=>OMEF nội tiếp

\(\text{a) Ta có:}\)
∠BFC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AFC = 90o
∠BEC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AEC = 90o
Tứ giác AEHF có:
∠AFC = 90o
∠AEC = 90o
=>∠AFC + ∠AEC = 180o
=> AEHF là tứ giác nội tiếp
b) ∠AFH = 90o => AH là đường kính đường tròn ngoại tiếp tứ giác AEHF
\(\text{Do đó trung điểm I của AH là tâm đường tròn ngoại tiếp tứ giác AEHF}\)
=> Bán kính đường tròn ngoại tiếp tứ giác AEHF là R = AI = \(\frac{AH}{2}\) = 2cm
Ta có: ∠BAC = 60o
=> ∠FIE = 2∠BAC = 120o (Góc nội tiếp bằng \(\frac{1}{2}\) góc ở tâm cùng chắn một cung)
=> Số đo ∠EHF = 120o
Diện tích hình quạt IEHF là:
\(S=\frac{\pi R^2N}{360}=\frac{\pi.2^2.120}{360}=\frac{4\pi}{3}\left(ĐVDT\right)\)
\(\text{c) Xét tam giác ABC có: }\)
BE và CF là các đường cao
BE giao với CF tại H
=> H là trực tâm tam giác ABC
=>AH ⊥ BC hay ∠ADC = ∠ADB = 90o
Xét tứ giác BEFC có:
∠BFC = ∠BEC = 90o
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc bằng nhau
=> BEFC là tứ giác nội tiếp
=> ∠HFE = ∠BEC ( 2 góc nội tiếp cùng chắn cung EC) (1)
Xét tứ giác BFHD có:
∠BFH = ∠HDB = 90o
=>∠BFH + ∠HDB = 180o
=> Tứ giác BFHD là tứ giác nội tiếp ( tổng 2 góc đối bằng 180o)
=> ∠DFH = ∠BEC ( 2 góc nội tiếp cùng chắn cung HD) (2)
Từ (1) và (2) = > ∠HFE = ∠DFH
=> FH tia phân giác của góc ∠DFE
d) Tam giác OFB cân tại O => ∠OFB = ∠FBO
Tam giác BFC vuông tại F => ∠FBO + ∠HCD = 90o
=> ∠OFB + ∠HCD = 90o (*)
\(\hept{\begin{cases}\Delta FIH\text{CÂN TẠI I}\\\widehat{IHF}=\widehat{DHC}\left(\text{ĐỐI ĐỈNH}\right)\\\Delta HDC\text{VUÔNG TẠI D}\Rightarrow\widehat{DHC}+\widehat{HDC}=90^0\end{cases}}\Rightarrow\widehat{IFH}+\widehat{HDC}=90^0\)
Từ (*) và (**) => ∠OFB = ∠IFH
=> ∠OFB + ∠OFH = ∠IFH + ∠OFH <=> ∠BFC = ∠FIO <=> ∠FIO) = 90o
Vậy FI là tiếp tuyến của (O)
Chứng minh tương tự EI là tiếp tuyến của (O)
Mà I là trung điểm của AH
=> Tiếp tuyến của (O) tại E và F và AH đồng quy tại 1 điểm.
HÌNH THÌ VÀO THỐNG KÊ HỎI ĐÁP CỦA MIK NHA
VCN JACK trả lời cuc64 kì đ luôn . đ là chất

A B C I S D E F G K L K' M x
Gọi giao điểm khác D của hai đường tròn (BED);(CFD) là K'; K'I cắt EF tại L; DL cắt (I;ID) tại M khác D.
Ta thấy IE = IF; AI là phân giác ngoài của ^EAF, từ đây dễ suy ra 4 điểm A,E,I,F cùng thuộc một đường tròn
Vì 3 điểm D,F,E lần lượt thuộc các cạnh BC,CA,AB của \(\Delta\)ABC nên (BED);(CFD);(AFE) đồng quy (ĐL Miquel)
Hay điểm K' thuộc đường tròn (AIFE). Do vậy LI.LK' = LE.LF = LD.LM (= PL/(G) = PL/(I) )
Suy ra 4 điểm K',M,I,D cùng thuộc một đường tròn. Mà ID = IM nên ^IK'D = ^IK'M.
Đồng thời ^DIM = 1800 - ^DK'M = 1800 - ^EK'F + 2.^FK'D = ^BAC + 2.^ACB = 2.^AID
Suy ra IA vuông góc DM, từ đó M,L,D,A thẳng hàng (Vì IA cũng vuông góc AD)
Khi đó dễ thấy AL là phân giác ^BAC, K'L là phân giác ^EK'F, mà tứ giác AEK'F nội tiếp
Suy ra AEK'F là tứ giác điều hòa, từ đây AK' là đường đối trung của \(\Delta\)AEF
Suy ra K' trùng K. Kẻ tiếp tuyến Kx của (G), ta có ^BKx = ^EKx - ^EKB = ^EFK - ^EFD = ^BCK
Do đó (BKC) tiếp xúc với (G) tại K, tức KG đi qua tâm của (BKC) (1)
Gọi S là trung điểm cung lớn BC của (ABC). Có SB = SC và ^BKC = ^AED + ^AFD = 1800 - ^BSC/2
Suy ra S là tâm của đường tròn (BKC) (2)
Từ (1) và (2) suy ra KG luôn đi qua S cố định (Vì S là trung điểm cùng BC lớn cố định) (đpcm).

A B C H D M
Tam giác ABC cân tại A, H là trung điểm của BC nên \(AH\perp BC\).
Có \(\overrightarrow{AM}.\overrightarrow{BD}=\dfrac{1}{2}\left(\overrightarrow{AH}+\overrightarrow{AD}\right)\left(\overrightarrow{BH}+\overrightarrow{HD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AH}.\overrightarrow{BH}+\overrightarrow{AH}.\overrightarrow{HD}+\overrightarrow{AD}.\overrightarrow{BH}+\overrightarrow{AD}.\overrightarrow{HD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AH}.\overrightarrow{HD}+\overrightarrow{AD}.\overrightarrow{BH}\right)\) (do \(AH\perp BC\) )
\(=\dfrac{1}{2}\overrightarrow{AH}.\left(\overrightarrow{BH}+\overrightarrow{HD}\right)+\dfrac{1}{2}\left(\overrightarrow{AH}+\overrightarrow{HD}\right).\overrightarrow{BH}\)
\(=\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{BH}+\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{HD}+\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{BH}+\dfrac{1}{2}\overrightarrow{HD}.\overrightarrow{BH}\)
\(=\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{HD}+\dfrac{1}{2}\overrightarrow{HD}.\overrightarrow{BH}\) ( do \(AH\perp BC\) )
\(=\dfrac{1}{2}\overrightarrow{HD}\left(\overrightarrow{AH}+\overrightarrow{BH}\right)\)
\(=\dfrac{1}{2}\overrightarrow{HD}\left(\overrightarrow{AH}+\overrightarrow{HC}\right)\) ( doM là trung điểm của BC).
\(=\dfrac{1}{2}\overrightarrow{HD}.\overrightarrow{AC}\)
\(=0\) (Do \(HD\perp AC\) )