Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b1 a) goi I la giao diem cua AD va BC
I A B C D
vi AB//DC => goc IDC = goc DAB (2 goc dong vi)
ma goc A =30 => goc IDC =30
lai co goc IDC + goc ADC =180 ( I,D,A thang hang)
30+ goc ADC =180 => goc ADC=150
vi AB//DC => goc ICD = goc CBA (2 goc dong vi)
có goc ICD+ goc DCB =180 (I,C,B thang hang )
goc ICD+ 120=180 => goc ICD = 60 => goc ABC=60
còn ý b) bạn làm tương tự nhé
b2
A B C D
vi DC =BC (gt) => tam giac DCB can tai C => goc CDB = goc DBC (1)
vi DB la phan giac cua goc ADC => g ADB =g BDC (2)
tu (1,2) => g ADB = g DBC
ma 2 goc nay o vi tri so le trong
=> AD// BC => ABCD la hinh thang

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
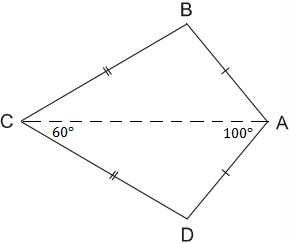
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000
Abcd là hình thang
Câu trả lời tương tự :
a, BM=BC, tam giác BMC cân tại C, nên góc MCN= góc CMB
Ta có góc BCM+góc MCA=90độ, góc CMH+góc MCH=90độ, suy ra gócMCH=góc MCN
Tam giác MHC=tam giác MNC(c.g.c), do đó góc MNC=góc MHC=90độ, vậy MNvuông góc AC(đpcm)
b, Ta có: BM=BC,CH=CN và AM>AN. Do đó:
BM+MA+CH>BC+CN+NA hay AB+CH>BC+CA
thêm cho bạn cái này nha: trong một tam giác vuông, tổng độ dài hai cạnh góc vuông nhỏ hơn tổng độ dài cạnh huyền và độ dài đường vuông góc kẻ từ đỉnh góc vuông xuống cạnh huyền