Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
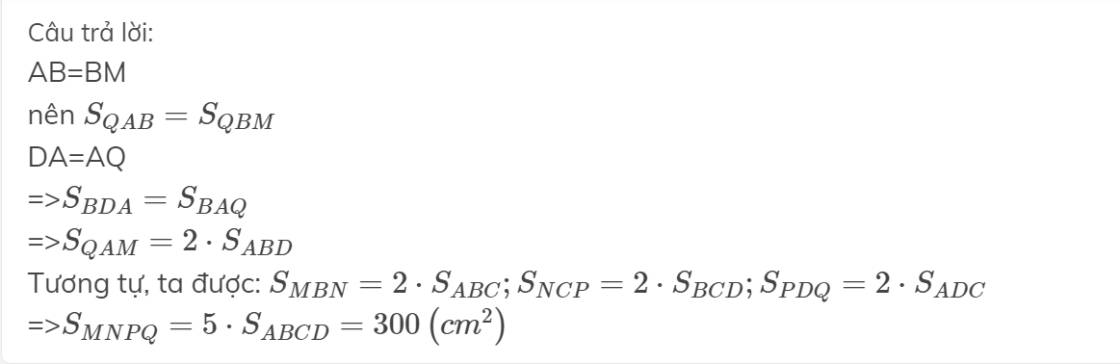
AB=BM
nên \(S_{QAB}=S_{QBM}\)
DA=AQ
=>\(S_{BDA}=S_{BAQ}\)
=>\(S_{QAM}=2\cdot S_{ABD}\)
Tương tự, ta được: \(S_{MBN}=2\cdot S_{ABC};S_{NCP}=2\cdot S_{BCD};S_{PDQ}=2\cdot S_{ADC}\)
=>\(S_{MNPQ}=5\cdot S_{ABCD}=300\left(cm^2\right)\)
Nối M với C; N với D; P với A và Q với B
Nối A với C; B với D
Ta có S(ABCD)=S(ABD)+S(BCD)=S(ABC)+S(ACD)
Xét tg ABQ và tg ABD có chung đường cao hạ từ B xuống DQ và cạnh đáy AQ=AD nên S(ABQ)=S(ABD)
Xét tg ABQ và tg BMQ có chung đường cao hạ từ Q xuống AM và cạnh đáy AB=BM nên S(ABQ)=S(BMQ)
=> S(ABQ)=S(BMQ)=S(ABD) => S(AMQ)=S(ABQ)+S(BMQ)=2xS(ABD) (1)
Chứng minh tương tự khi xét các tam giác BCD với tg CDN và tg CDN với tg DNQ => S(CNP)=2xS(BCD) (2)
Từ (1) và (2) => S(AMQ)+S(CNP)=2xS(ABD)+2xS(BCD)=2x[S(ABD)+S(BCD)]=2xS(ABCD)
Chứng minh tương tự ta sẽ có kết quả S(DPQ)+S(CMN)=2x[S(ACD)+S(ABC)]=2xS(ABCD)
S(MNPQ)=[S(AMQ)+S(CNP)]+[S(DPQ)+S(CMN)]+S(ABCD)=5xS(ABCD)=5x25=125 cm2
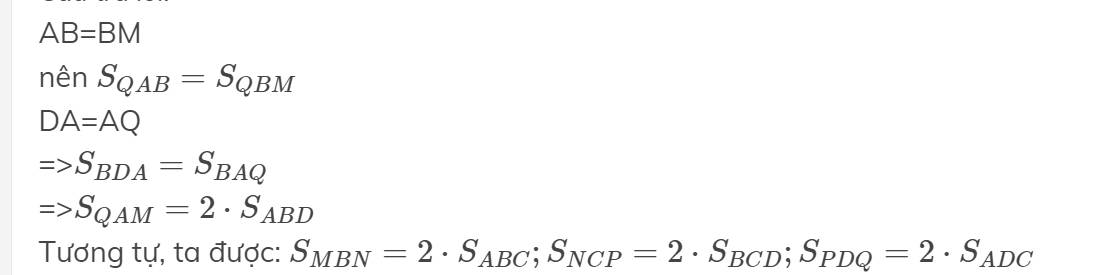
=>\(S_{MNPQ}=S_{MBN}+S_{NCP}+S_{PDQ}+S_{QMA}+S_{ABCD}\)
\(=5\cdot S_{ABCD}=5\cdot25=125\left(cm^2\right)\)
MQ kéo dài cắt DC tại F; MN kéo dài cắt DC tại E
Ta có diện tích hình thang ABCD bằng diện tích tam giác FME
S∆ MPF = S∆ MPE (đáy bằng nhau, đường cao chung)
S∆ MNP = S∆NPE (đáy MN = NE, đường cao chung)
S∆PMQ = S∆PQF (đáy MN = NE, đường cao chung)
Nên SMNPQ = 1/2 S ∆FME hay S(MNPQ) =1/2 S(ABCD)
= 60 : 2 = 30 (cm2)
Đáp số: 30 cm2
