Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
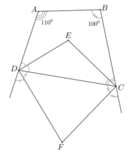
Trong tứ giác ABCD, ta có: ∠ A + ∠ B + ∠ C + ∠ D = 360 °
⇒ ∠ C + ∠ D = 360 ° - ( ∠ A + ∠ B) = 360 ° – ( 110 ° + 100 ° ) = 150 °
Do DE và CE lần lượt là tia phân giác của góc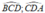 
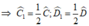
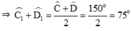
Trong ΔCED ta có:
∠ CED = 180o – ∠ C 1 + ∠ D 1 = 180 ° - 75 ° = 105 °
DE ⊥ DF (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ EDF = 90 °
CE ⊥ CF (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ ECF = 90 °
Trong tứ giác CEDF, ta có: ∠ DEC + ∠ EDF + ∠ DFC + ∠ ECF = 360 °
⇒ ∠ DFC = 360 ° - ( ∠ DEC + ∠ EDF + ∠ ECF) = 360 ° - 105 ° - 90 ° - 90 ° = 75 °
Bạn tham khảo tại đây:
Bài 8 Sách bài tập - trang 80 - Toán lớp 8 | Học trực tuyến
Bạn chú ý cái đường link rồi sửa thành h là OK hết chỗ nói nha.Hoặc là ib với mik rồi mik cho:3