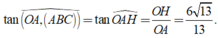Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


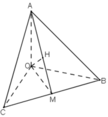
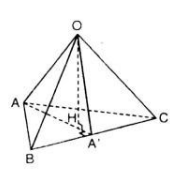
a) Ta có:
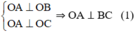
Do H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC) nên:
OH ⊥ (ABC) ⇒ OH ⊥ BC (2)
Mà OA; OH ⊂ (OAH); OA ∩ OH = O (3)
Từ (1); (2) và (3) ⇒ BC ⊥ (OAH)
⇒ BC ⊥ AH
Chứng minh tương tự ta có: AC ⊥ BH
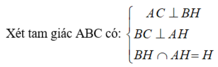
⇒ H là trực tâm ΔABC.
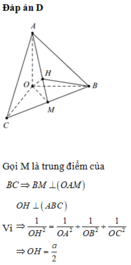
b) Gọi M = AH ∩ BC.
+ BC ⊥ (OAH) ⇒ BC ⊥ OM.
ΔOBC vuông tại O có đường cao OM
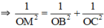
+ OA ⊥ (OBC) ⇒ OA ⊥ OM ⇒ ΔOAM vuông tại O.
OH ⊥ (ABC) ⇒ OH ⊥ AM.
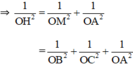

Chúng ta biết rằng tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Vì vậy, ta có thể xem tứ diện OABC là một hình chữ nhật với cạnh OA, OB, OC.
Gọi SABC là diện tích của hình chữ nhật OABC. Ta có:
SABC = OA x OB
Gọi SHBC là diện tích của tam giác HBC. Ta có:
SHBC = 1/2 x HB x BC
Vì tứ diện OABC là một hình chữ nhật, nên ta có:
SOAB = OA x OB
Vậy, ta có:
(SOAB)2 = (OA x OB)2
= OA2 x OB2
= SABC x SHBC
= SABC + SHBC
Vậy, ta đã chứng minh được rằng (SOAB)2 = SABC + SHBC.

a: OA\(\perp\)OB
OA\(\perp\)OC
OB,OC cùng thuộc mp(OBC)
Do đó: OA\(\perp\)(OBC)
b: Ta có: BC\(\perp\)AK
BC\(\perp\)AO
AK,AO cùng thuộc mp(AKO)
Do đó: BC\(\perp\)(AKO)
=>BC\(\perp\)OH
Ta có: OH\(\perp\)BC
OH\(\perp\)AK
AK,BC cùng thuộc mp(ABC)
Do đó: OH\(\perp\)(ABC)