


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





làm đc chưa bạn...
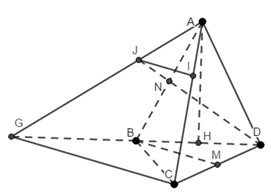
gọiE là tđ AD
suy ra NA = NH = NMNM
gọi F là tđ AM thì c/m đc KN KM KA KD bằng nhau
vậy AMN cân vuông tại N

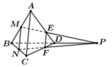
Do E, F lần lượt là trọng tâm các tam giác ABP, BCP nên
Chọn B.

Đáp án A
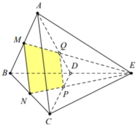
Nối ![]() chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
Dễ thấy P,Q lần lượt là trọng tâm của ∆BCE, ∆ABE
Gọi S là diện tích 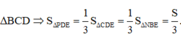
Họi h là chiều cao của tứ diện ABCD 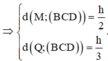
Khi đó 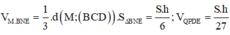
Suy ra
![]()
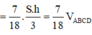


Đáp án C
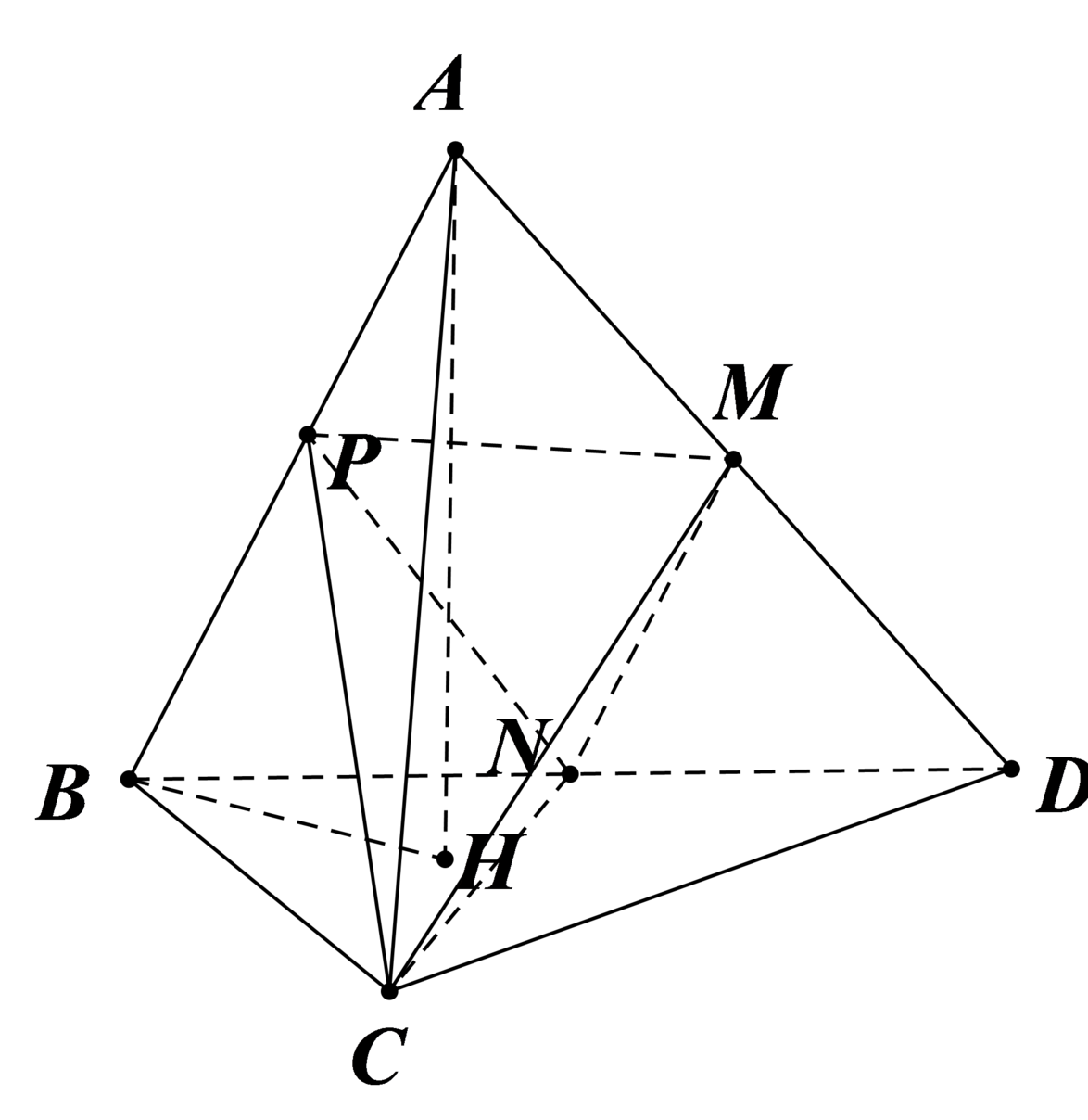
Gọi H là trọng tâm Δ B C D thì A H ⊥ B C D .
Ta có: B H = 2 3 . 3 3 2 = 3
⇒ A H = A B 2 − B H 2 = 9 − 3 = 6
Do đó: V A B C D = 1 3 . A H . S B C D = 1 3 . 6 . 3 2 3 4 = 9 2 4 .
Lại có:
V C . M N P V C . A B D = 1 3 d C , A B D . S M N P 1 3 d C , A B D . S A B D = S M N P S A B D = S A B D − S S P M − S D M N − S B P N S A B D = 1 − 1 2 . 2017 4035 − 1 4 − 1 2 . 2018 4035 = 1 4
Vậy V C . M N P = 1 4 . 9 2 4 = 9 2 16 .

Đáp án D
Gọi I và J lần lượt là trung điểm AB,CD. Tính khoảng cách giữa đường thẳng IJ và (SAD).
S A ⊥ A D , A B ⊥ S A D ,IJ// S A D ⇒ d IJ; S A D = d I; S A D = I A = a 2