Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

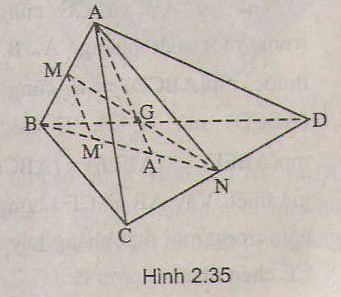
a) Có: MN ⊂ (ABN)
⇒ G ∈ (ABN)
⇒ AG ⊂ (ABN).
Trong (ABN), gọi A’ = AG ∩ BN.
⇒ A’ ∈ BN ⊂ (BCD)
⇒ A’ = AG ∩ (BCD).
b) + Mx // AA’ ⊂ (ABN) ; M ∈ (ABN)
⇒ Mx ⊂ (ABN).
M’ = Mx ∩ (BCD)
⇒ M’ nằm trên giao tuyến của (ABN) và (BCD) chính là đường thẳng BN.
⇒ B; M’; A’ thẳng hàng.
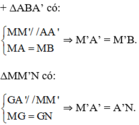
⇒ BM’ = M’A’ = A’N.
c) Áp dụng chứng minh câu b ta có:
ΔMM’N có: MM’ = 2.GA’
ΔBAA’ có: AA’ = 2.MM’
⇒ AA’ = 4.GA’
⇒ GA = 3.GA’.

Cau 33:
\(\left|\overrightarrow{u}-\overrightarrow{v}\right|=\sqrt{\left(\overrightarrow{u}-\overrightarrow{v}\right)^2}=\sqrt{u^2+v^2-2\cdot u\cdot v\cdot cos120}\)
\(=\sqrt{4^2+3^2-2\cdot4\cdot3\cdot\dfrac{-1}{2}}=\sqrt{37}\)

a, Tứ diện ABCD đều cạnh a.
Đặt \(\vec{AB}=\vec{x};\vec{AC}=\vec{y};\vec{AD}=z\)
\(\Rightarrow\vec{x}.\vec{y}=\vec{y}.\vec{z}=\vec{z}.\vec{x}=\dfrac{a^2}{2}\)
\(\Rightarrow\vec{CD}=\vec{AD}-\vec{AC}=\vec{z}-\vec{y}\)
\(\vec{AG}=\vec{AB}+\vec{BG}\)
\(=\vec{AB}+\dfrac{1}{3}\left(\vec{BD}+\vec{BC}\right)\)
\(=\vec{AB}+\dfrac{1}{3}\left(\vec{AD}-\vec{AB}+\vec{AC}-\vec{AB}\right)\)
\(=\dfrac{1}{3}\vec{AB}+\dfrac{1}{3}\vec{AC}+\dfrac{1}{3}\vec{AD}\)
\(=\dfrac{1}{3}\vec{x}+\dfrac{1}{3}\vec{y}+\dfrac{1}{3}\vec{z}\)
\(\Rightarrow\vec{CD}.\vec{AG}=\dfrac{1}{3}\left(\vec{z}-\vec{y}\right)\left(\vec{x}+\vec{y}+\vec{z}\right)\)
\(=\dfrac{1}{3}\vec{z}\left(\vec{x}+\vec{y}+\vec{z}\right)-\dfrac{1}{3}\vec{y}\left(\vec{x}+\vec{y}+\vec{z}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{a^2}{2}+\dfrac{a^2}{2}+a^2\right)-\dfrac{1}{3}\left(\dfrac{a^2}{2}+a^2+\dfrac{a^2}{2}\right)\)
\(=0\)
\(\Rightarrow AG\perp CD\)

a. theo đề ta có ngay kết luận rằng: \(AG\perp CD\) vì ABCD là hình chóp tam giác đều.
b. Gọi N là trug điểm AD , ta có:
MN // AC \(\Rightarrow\left(AC,BM\right)=\widehat{BMN}\)
Xét \(\Delta BMN\) có
\(BM=\dfrac{a\sqrt{3}}{2}\) ( vì BM là trug tuyến trog ΔBCD đều)
\(BN=\dfrac{a\sqrt{3}}{2}\) ( vì Bn là trug tuyến trog ΔABD đều)
\(MN=\dfrac{1}{2}AC=\dfrac{a}{2}\) , vì MN là đường tb trog Δ ACD
\(cos\widehat{BMN}=\dfrac{MB^2+MN^2-BN^2}{2MB.MN}=\dfrac{MN}{2MB}=\dfrac{\dfrac{a}{2}}{2.\dfrac{a\sqrt{3}}{2}}=\dfrac{\sqrt{3}}{6}\)
Vậy ta được : \(cos\left(AC,BM\right)=\dfrac{\sqrt{3}}{6}\)
Còn cách giải khác nữa , mà nó dài nen t lm cách này cho nhanh có gì k hỉu thì hỏi .

a: Xét ΔAMB có ME là đường phân giác
nên AE/EB=AM/MB=AM/MC(4)
XétΔAMC có MD là đường phân giác
nên AD/DC=AM/MC(5)
Từ (4) và (5) suy ra AE/EB=AD/DC
b: Xét ΔABC có
AE/EB=AD/DC
nên ED//BC
Xét ΔABM có EI//BM
nên EI/BM=AE/AB(1)
Xét ΔACM có ID//MC
nên ID/MC=AD/AC(2)
Xét ΔABC có
ED//BC
nên AE/AB=AD/AC(3)
Từ (1), (2) và (3) suy ra EI/BM=DI/MC
mà BM=CM
nên EI=DI
hay I là trung điểm của ED