Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

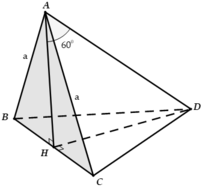
ban cm AH _|_mp (BCD) tương tự như trên ==> AH_|_DH, hai tg ABC va BCD la 2 tg đều có cạnh Bc chung nên đường cao của chúng bằng nhau=> tg HAD vuông cân tại H ma AD =a => Ah =Dh =sin45*a = a\(\frac{\sqrt{2}}{2}\)
tg đều biết độ dài đường cao => độ dài mỗi cạnh, tu do tinh duoc dt tg ABC va tinh duoc the tich khoi chop

Chọn A
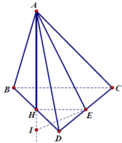
Coi như a = 1 . Tam giác ACD vuông tại A nên A D = C D 2 - A C 2 = 1 = A B cân tại A và tam giác ACD vuông cân tại A. Gọi H, E lần lượt là trung điểm của BD và DC. Ta có A H ⊥ B C D và C D ⊥ A E . Hơn nữa C D ⊥ A H ⇒ C D ⊥ A H E ⇒ C D ⊥ H E mà HE song song với BC suy ra BC vuông góc với CD. H là tâm của đường tròn ngoại tiếp tam giác BCD, do đó AH là trục đường tròn này. Trong tam giác AHE dựng đường thẳng qua E vuông góc AE và cắt AH tại điểm I. Do mặt phẳng (AHE) vuông góc với mặt phẳng (ACD) nên d cũng vuông góc với (ACD). Hơn nửa E là tâm của đường tròn ngoại tiếp tam giác ACD suy ra I là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Ta có A I . A H = A E 2 ⇒ A I = A E 2 A H . Ta có A E = 1 2 C D = 2 2 , H K = 1 2 B C = 1 2 ⇒ A H = 1 2
Vậy A I = A E 2 A H = 1 ⇒ R = 1 ⇒ V m c = 4 3 πa 3

S A B H C
Tam giác ABC vuông cân tại A nên \(BC=2AH=2a\)
Từ đó \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}a.2a=a^2\)
Vì \(SA\perp\left(ABC\right);AH\perp BC\) suy ra \(SH\perp BC\)
Do đó : \(\left(\left(SBC\right),\right)\left(ABC\right)=\widehat{SHA}=60^0\)
Suy ra \(SA=AH.\tan60^0=a\sqrt{3}\)
Vậy \(V_{SABC}=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}a\sqrt{3}a^2=\frac{a^3\sqrt{3}}{3}\)


Vậy \(SB^2=\dfrac{6a^2}{9}+4a^2=\dfrac{42a^2}{9}\)
Do đó \(SB=\dfrac{a\sqrt{42}}{3}\)
Ta suy ra :
\(r=\dfrac{SB}{2}=\dfrac{a\sqrt{42}}{6}\)

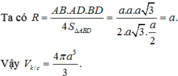
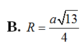
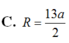


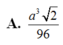
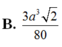
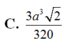
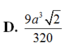

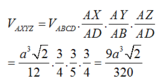
Đáp án C