K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 2 2020
\(CD=\sqrt{AC^2+AD^2}=a\sqrt{2}\)
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cos\widehat{BAC}}=a\sqrt{3}\)
\(\Rightarrow BD^2+CD^2=BC^2\Rightarrow CD\perp BD\)
\(cos\widehat{ADC}=\frac{AD}{CD}=\frac{1}{\sqrt{2}}\)
\(cos\left(\overrightarrow{AB};\overrightarrow{CD}\right)=\frac{\overrightarrow{AB}.\overrightarrow{CD}}{AB.CD}=\frac{\left(\overrightarrow{AD}+\overrightarrow{DB}\right).\overrightarrow{CD}}{a^2\sqrt{2}}=\frac{\overrightarrow{AD}.\overrightarrow{CD}}{a^2\sqrt{2}}=\frac{a.a\sqrt{2}.\frac{1}{\sqrt{2}}}{a^2\sqrt{2}}=\frac{1}{\sqrt{2}}\)
\(\Rightarrow\left(\overrightarrow{AB};\overrightarrow{CD}\right)=45^0\)

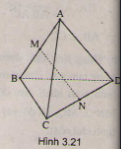
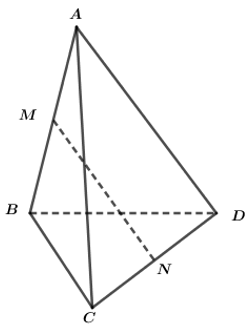



\(\left\{{}\begin{matrix}\widehat{BAC}=60^0\\AB=AC\end{matrix}\right.\) \(\Rightarrow\Delta ABC\) đều \(\Rightarrow AB=BC\)
Tương tự ta có \(\Delta ABD\) đều \(\Rightarrow BD=AB=BC\)
\(\Rightarrow\Delta ACD=\Delta BCD\left(c.c.c\right)\)
\(\Rightarrow AJ=BJ\) (cùng là trung tuyến của 2 tam giác bằng nhau)
\(\Rightarrow\Delta ABJ\) cân tại J
\(\Rightarrow IJ\perp AB\)
Dữ kiện \(\widehat{CAD}=90^0\) là ko cần thiết
P/s: quên vẽ hình
Thế còn đáp án?