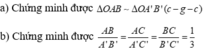Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
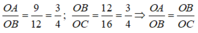
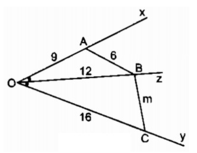
Xét △ OAB và △ OBCcó:
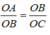
∠ AOB = ∠ BOC (OB là tia phân giác góc AOC)
Suy ra △ OAB đồng dạng với △ OBC (c.g.c)
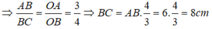
Chọn B

a: Xet ΔOCB và ΔOAD có
OC/OA=OB/OD
góc O chung
=>ΔOCB đồng dạng với ΔOAD
b: ΔOCB đồng dạng với ΔOAD
=>góc OCB=góc OAD
=>góc IAB=góc ICD
=>góc IBA=góc IDC; góc AIB=góc CID

a: Xet ΔOCB và ΔOAD có
OC/OA=OB/OD
góc O chung
=>ΔOCB đồng dạng với ΔOAD
b: ΔOCB đồng dạng với ΔOAD
=>góc OCB=góc OAD
=>góc IAB=góc ICD
=>góc IBA=góc IDC; góc AIB=góc CID

Ta có hình vẽ:
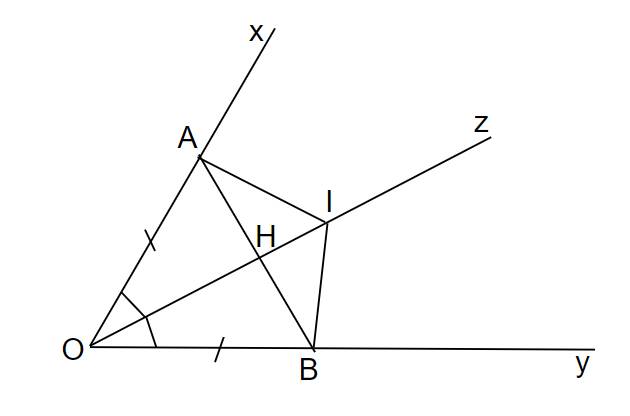
a) Vì Oz là phân giác của xOy nên xOz=yOz=xOy2���=���=���2
Xét Δ AOI và Δ BOI có:
OA = OB (gt)
AOI = BOI (cmt)
OI là cạnh chung
Do đó, Δ AOI = Δ BOI (c.g.c) (đpcm)
b) Xét Δ AOH và Δ BOH có:
OA = OB (gt)
AOH = BOH (câu a)
OH là cạnh chung
Do đó, Δ AOH = Δ BOH (c.g.c)
=> AHO = BHO (2 góc tương ứng)
Mà AHO + BHO = 180o (kề bù) nên AHO = BHO = 90o
=> AB⊥OI(đpcm))

OM=12-2=10cm
Xét ΔOBA có MN//BA
nên OM/MA=ON/NB
=>ON/NB=10/2=5
=>ON=5NB
mà ON+NB=18
nên ON=5/6*18=15cm