K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

P
Phong
CTVHS
8 tháng 5 2023
Khoảng cách từ ảnh đến thấu kính là:
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{d.f}{d-f}=\dfrac{8.4}{8-4}=8\left(cm\right)\)
Chiều cao của ảnh:
Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{8.2}{8}=2\left(cm\right)\)
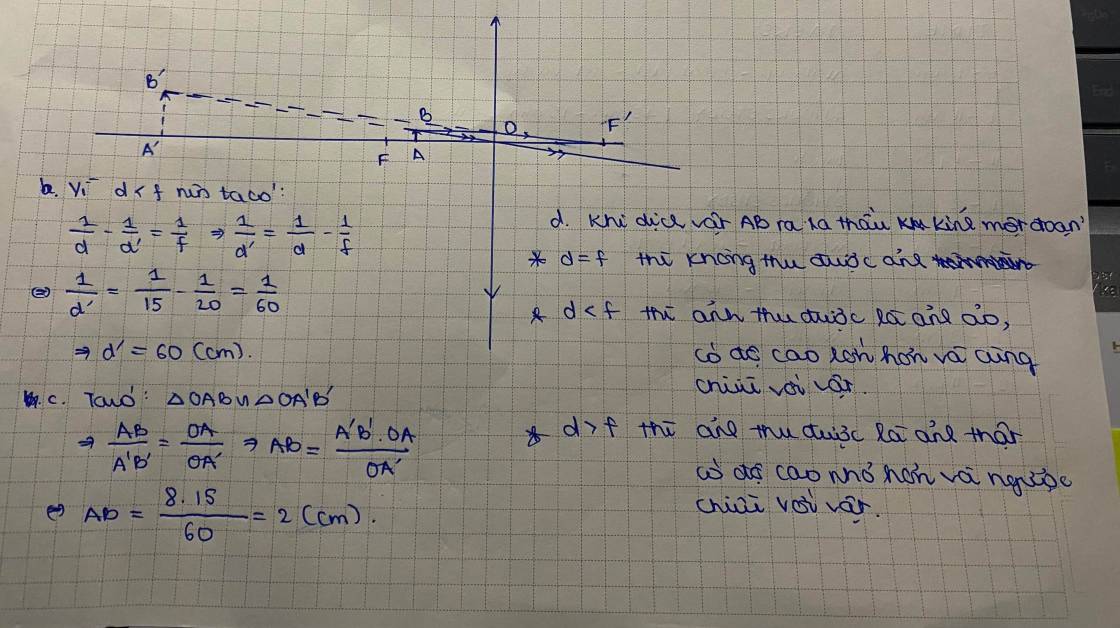

a) Tính chất:
- Ảnh thật
- Ảnh lớn hơn vật
- Ngược chiều với vật
b)
Tóm tắt:
OF = OF' = f = 16cm
AB = h = 4cm
OA = d = 24cm
A'B' = h' = ?
OA' = d' = ?
Giải:
\(\Delta ABF~\Delta OIF\)
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{AO-OF}{OF}\Leftrightarrow\dfrac{4}{A'B'}=\dfrac{24-16}{16}\)
=> A'B' = 8cm
\(\Delta OAB~\Delta OA'B'\)
\(\Rightarrow\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\Leftrightarrow\dfrac{24}{OA'}=\dfrac{4}{8}\Rightarrow OA'=48cm\)