Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{8}+\dfrac{1}{d'}\Rightarrow d'=24cm\)
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{8}{24}\Rightarrow h'=9cm\)
b)\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{12}+\dfrac{1}{d'}\Rightarrow d'=12cm\)
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{12}{12}\Rightarrow h'=3cm\)
c)\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{4}+\dfrac{1}{d'}\Rightarrow d'=-12cm\)
\(\Rightarrow TH\) không xảy ra.
d)\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{18}+\dfrac{1}{d'}\Rightarrow d'=9cm\)
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{18}{9}\Rightarrow h'=1,5cm\)
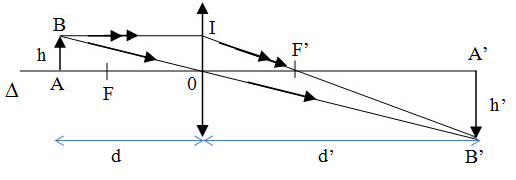
Hình vẽ thì em tham khảo nhé!
Áp dụng công thức: \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\) và độ cao ảnh \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
a) \(\dfrac{1}{6}=\dfrac{1}{8}+\dfrac{1}{d'}\Rightarrow d'=24cm\)
Độ cao ảnh: \(\dfrac{h}{h'}=\dfrac{8}{24}=\dfrac{1}{3}\)
Đề không cho độ cao vật nên chị làm đến đây, nếu có cho thì em thay vào h rồi tính h' là chiều cao ảnh cần tìm

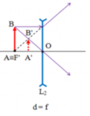
Vật AB đặt trước thấu kính phân kỳ có tiêu cự f, có A nằm trên trục chính và cách thấu kính một khoảng OA cho ảnh A′B′ cao bằng nửa vật AB khi OA=OF′=f
Đáp án: B