Question

[Hoàng Thị Hương Giang]

Cho tập hợp A=\(\left\{x\in R;\frac{1}{|x-1|}>2\right\}\).Xác định tập hợp R/A và biểu diễn trên trục số.

Answer 1

[Akai Haruma]

Lời giải:

\(\frac{1}{|x-1|}>2\Leftrightarrow \left\{\begin{matrix} |x-1|\neq 0\\ |x-1|< \frac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\neq 1\\ \frac{-1}{2}< x-1< \frac{1}{2}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 1\\ \frac{1}{2}< x< \frac{3}{2}\end{matrix}\right.\)

\(\Rightarrow A=(\frac{1}{2}; \frac{3}{2})\setminus \left\{1\right\}\)

\(\Rightarrow R\setminus A=(-\infty;\frac{1}{2}]\cup [\frac{3}{2};+\infty)\cup \left\{1\right\}\)

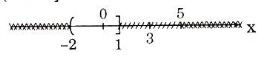
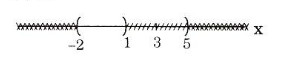
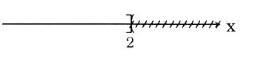
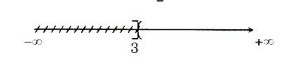
Hình: