Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

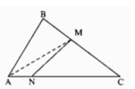
Kẻ đoạn thẳng AM. Xét tam giác MAC. Chứng minh tương tự như bài 1.4 ta có MN < a, trong đó a là đoạn lớn nhất trong hai đoạn thẳng MA và MC. Nếu ta chứng minh được
MA < AC và MC < AC thì sẽ suy ra được a < AC, từ đó có MN < AC.
Trong tam giác ABC có AB ≤ AC, M ∈ BC (M ≠ B, M ≠ C); Chứng minh tương tự bài 1.4, ta có AM < AC. Mặt khác MC < BC ≤ CA. Vậy a < AC, suy ra MN < AC.

a: ΔCAM cân tại C
=>góc CAM=góc CMA
b: góc HAM+góc CMA=90 độ
góc BAM+góc CAM=90 độ
mà góc CMA=góc CAM
nên góc HAM=góc BAM
=>ĐPCM
c: Xét ΔAHM và ΔANM có
AH=AN
góc HAM=góc NAM
AM chung
=>ΔAHM=ΔANM
=>góc AHM=góc ANM=90 độ
=>MN vuông góc AB

A B C M I H N
- Hạ \(BI\perp AC\)và \(MH\perp AC\)
Xét \(\Delta BIC\)và \(\Delta MHN\)có:
\(HN< IC\)
\(HM< BI\)
\(MN^2=HN^2+HM^2\)
\(BC^2=BI^2+IC^2\)
\(\Rightarrow MN< BC\)
Mà \(BC< AC\Rightarrow MN< BC\)
Cách 2: Xét \(\Delta MHN\)và \(\Delta MHC\)có:
MH chung
HN<HC
\(\hept{\begin{cases}MN^2=MH^2+HN^2\\MC^2=MH^2+HC^2\end{cases}\left\{MN< MC\right\}}\)
Mà MC<BC<AC => MN<AC