Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Em tự giải
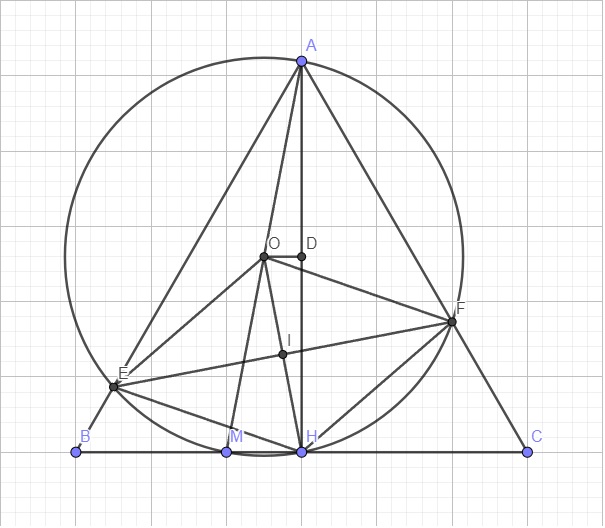
b. Do tam giác ABC đều và AH là đường cao \(\Rightarrow AH\) đồng thời là phân giác góc A
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.60^0=30^0\)
AEMHF nội tiếp đường tròn tâm O \(\Rightarrow\widehat{HOF}=2.\widehat{CAH}=60^0\) (góc nội tiếp và góc ở tâm cùng chắn cung HF)
Mà \(OH=OF\) (cùng là bán kính) \(\Rightarrow\Delta OHF\) đều (tam giác cân có 1 góc 60 độ)
Tương tự ta có \(\widehat{HOE}=60^0\Rightarrow\Delta OHE\) đều
\(\Rightarrow OE=OF=HE=HF\Rightarrow OEHF\) là hình thoi
c.
Gọi D là trung điểm AH \(\Rightarrow OD\perp AH\) \(\Rightarrow OH\ge DH\Rightarrow OH\ge\dfrac{1}{2}AH\Rightarrow OH\ge\dfrac{a\sqrt{3}}{2}\)
Gọi I là giao điểm EF và OH \(\Rightarrow I\) là tâm hình thoi OEHF
\(S_{OEHF}=2S_{OHE}=2EI.OH=2\sqrt{OE^2-OI^2}.OH\)
\(=2OH.\sqrt{OH^2-\left(\dfrac{OH}{2}\right)^2}=OH^2\sqrt{3}\ge\left(\dfrac{a\sqrt{3}}{2}\right)^2.\sqrt{3}=\dfrac{3a^2\sqrt{3}}{2}\)
Dấu "=" xảy ra khi \(OH=DH\Leftrightarrow O\) trùng D
\(\Rightarrow M\) trùng H

a: Xét ΔBAC có \(AC^2=BA^2+BC^2\)
nên ΔBAC vuông tại B
b: Xét ΔBAC vuông tại B có
\(sinA=\dfrac{BC}{CA}=\dfrac{42}{58}=\dfrac{21}{29}\)
\(cosA=\dfrac{AB}{AC}=\dfrac{40}{58}=\dfrac{20}{29}\)
\(tanA=\dfrac{BC}{BA}=\dfrac{21}{20}\)
\(cotA=\dfrac{BA}{BC}=\dfrac{20}{21}\)
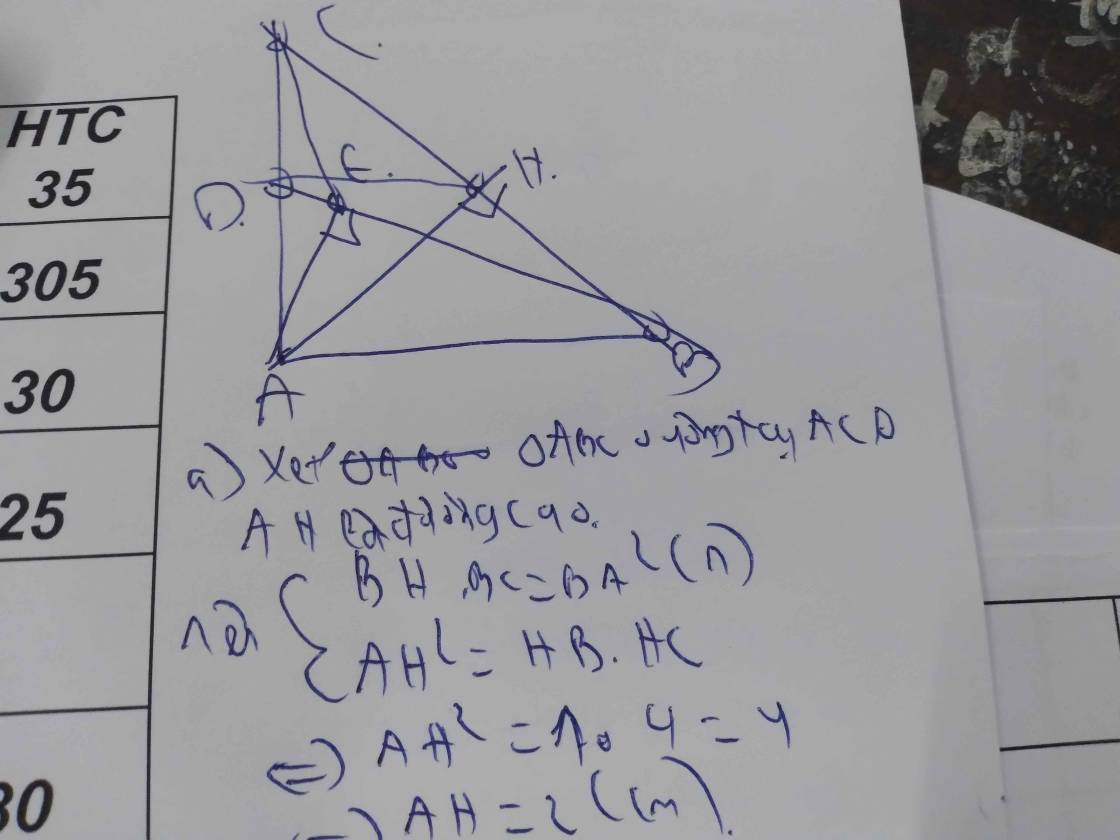
c: Xét ΔBAC vuông tại B có BH là đường cao
nên \(BH\cdot AC=BA\cdot BC\)
=>\(BH\cdot58=40\cdot42=1680\)
=>\(BH=\dfrac{840}{29}\left(cm\right)\)
Xét ΔBAC vuông tại B có BH là đường cao
nên \(BA^2=AH\cdot AC\)
=>\(AH\cdot58=40^2=1600\)
=>\(AH=\dfrac{800}{29}\left(cm\right)\)
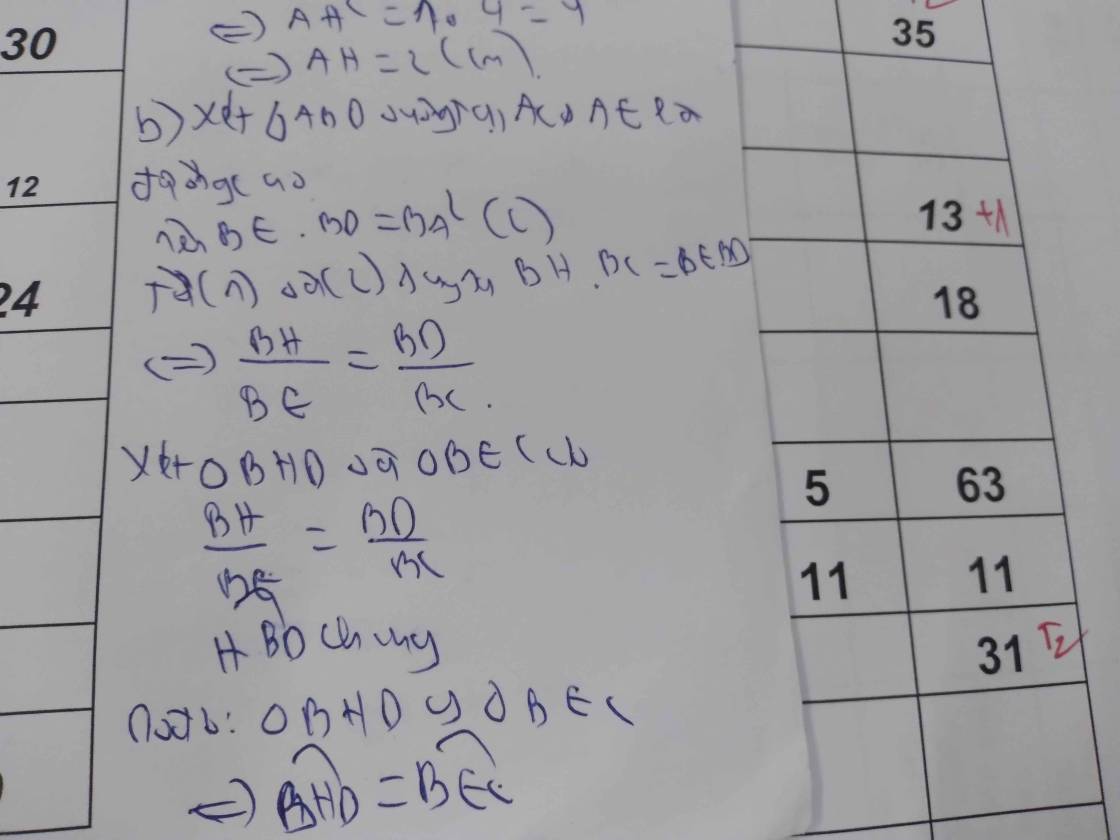
Xét ΔBHA vuông tại H có HE là đường cao
nên \(\left\{{}\begin{matrix}HE\cdot BA=HB\cdot HA\\BE\cdot BA=BH^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}HE\cdot40=\dfrac{840}{29}\cdot\dfrac{800}{29}\\BE\cdot40=\left(\dfrac{840}{29}\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}HE=\dfrac{16800}{841}\left(cm\right)\\BE=\dfrac{17640}{841}\left(cm\right)\end{matrix}\right.\)
Xét tứ giác BEHF có
\(\widehat{BEH}=\widehat{BFH}=\widehat{FBA}=90^0\)
=>BEHF là hình chữ nhật
=>\(BF=HE=\dfrac{16800}{841}\left(cm\right)\)
d: Xét tứ giác BPMQ có
\(\widehat{BPM}=\widehat{BQM}=\widehat{QBP}=90^0\)
=>BPMQ là hình chữ nhật

Trả lời :
Hình bạn tự phác ra nhé.
Vì \(\widehat{EAF}+\widehat{EHF}=180^o\)
=> Tứ giác AEHF nội tiếp đường tròn.
\(\Rightarrow\widehat{EAH}=\widehat{EFH}\)(1)
Mặt khác, \(\widehat{EHF}=\widehat{BAC}=90^o\)(2)
Từ (1) và (2) => \(\Delta ABC~\Delta HEF\)(g.g)
\(\Rightarrow\frac{AB}{HE}=\frac{BC}{EF}\)
=> HE . BC = EF . AB (đpcm)