
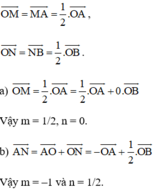
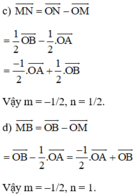
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

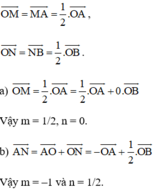
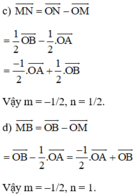

b)
O B A M N
\(\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AO}=-\dfrac{1}{2}\overrightarrow{OA}\)
Vậy \(m=-\dfrac{1}{2};n=0\).
c)
\(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AB}=\dfrac{1}{2}\left(\overrightarrow{AO}+\overrightarrow{OB}\right)=-\dfrac{1}{2}\overrightarrow{OA}+\dfrac{1}{2}\overrightarrow{OB}\).
Vậy \(m=-\dfrac{1}{2};n=\dfrac{1}{2}\).
d)
\(\overrightarrow{MB}=\dfrac{1}{2}\overrightarrow{OB}\)
Vậy \(m=0;n=\dfrac{1}{2}\).


bẹn tự vẽ hình nhé! Gọi I và J lần lượt là trung điểm của AD và BC.
Theo giả thiết: \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{O}a\)
\(\Leftrightarrow2\left(\overrightarrow{OI}+\overrightarrow{OJ}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\)O,I, J thẳng hàng.(1)
\(\Delta OAD\)cân tại \(O\Rightarrow OI\perp AB\)(2)
\(\Delta OBC\)cân tại \(O\Rightarrow OJ\perp BC\)(3)
Từ 1,2,3 => AD//BC
Tương tự ta chứng minh được AB//CD
Vậy tứ giáo ABCD nội tiếp được trong đường tròn, nên tứ giác ABCD là hình chữ nhật. (đpcm)
Thanks Đặng Ngọc Quỳnh
P/s:trc chỗ (2) hình như là OI vuông góc với AD mới đúng :P


a) Dãy các số liệu chiều cao của các học sinh nam ở bảng 5 có :
\(\overline{x_1}\approx163\left(cm\right);s_1^2\approx134,3;s_1\approx11,59\)
Dãy các số liệu chiều cao của các học sinh nữ cho ở bảng 5 có :
\(\overline{x_2}\approx159,5\left(cm\right);s_2^2\approx148;s_2\approx12,17\)
b) Nhóm T có \(\overline{x_3}=163\left(cm\right);s_3^2=169;s_3=13\)
Học sinh ở nhóm nam và nhóm T có chiều cao như nhau và cùng lớn hơn chiều cao của học sinh ở nhóm nữ (vì \(\overline{x}_1=\overline{x}_3>\overline{x}_2\)
Vì \(\overline{x}_1=\overline{x}_3=163\left(cm\right)\) và \(s_1< s_3\) nên chiều cao của các học sinh nam đồng đều hơn chiều cao của các học sinh nhóm T