Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẼ hình nha
Gọi N là giao điểm của CE và AB
Xét CME và BMD có
MB=MC(giả thiết )
MD=ME(giả thiết)
BMD=CME(2 góc đối đỉnh)
Do đó CME=BMD(c.g.c)
=>MBD=MCE => BD // CE
=> DBN+CNB=180 (2 gõc trong cùng phía bù nhau)
=>CNB=180-CNB=180-90=90
Vậy CE vuông góc với AB

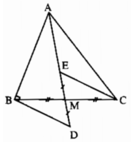
+) Xét ΔBMD và ΔCME có:
BM = MC (vì M là trung điểm BC)
MD = ME (giả thiết)
∠BMD = ∠EMC (hai góc đối đỉnh)
⇒ ΔBMD = ΔCME (c.g.c)
⇒ ∠D = ∠MEC (hai góc t.ư)
Mà hai góc này ở vị trí so le trong nên suy ra BD // CE.
Ta có AB ⊥ BD (giả thiết) và BD // CE (chứng minh trên) nên AB ⊥ CE

Bạn tự vẼ hình nha
Gọi N là giao điểm của CE và AB
Xét CME và BMD có
MB=MC(giả thiết )
MD=ME(giả thiết)
BMD=CME(2 góc đối đỉnh)
Do đó CME=BMD(c.g.c)
=>MBD=MCE => BD // CE
=> DBN+CNB=180 (2 gõc trong cùng phía bù nhau)
=>CNB=180-CNB=180-90=90
Vậy CE vuông góc với AB
xét tam giác EMC và tam giác DMB
có góc EMC=góc DMB
ME=MD(GT)
MB=MC (GT)
=>tam giác EMC=Tam giác DMB(c.g.c)
=>goc CEM= goc DBM (2goc tuong ung)
ma go CEM va Goc DBM la 2 goc SLT
=>AC song song BD
và Góc ABD=90 do (GT)
=> góc AHC =90 do ( 2goc đồng vị )
vậy CE vuông góc với AB tại H

Xét \(\Delta BMD \) và \(\Delta CME \) có:
ME = MD (gt)
BM = CM ( vì M là trung điểm của BC)
\(\widehat{DMB}=\widehat{EMC}\) (đối đỉnh)
Do đó: \(\Delta BMD \) = \(\Delta CME \) (c.g.c)
=> \(\widehat{BDM}=\widehat{MEC}\) (2 góc tương ứng)
mà 2 góc \(\widehat{BMD}\) và \(\widehat{MEC}\)nằm ở vị trí so le trong
=> BD // CE.
Ta có:\(AB\perp BD\) , BD // CE
=> AB \(\bot\) CE.

a) Xét ΔBMD và ΔCME có
BM=CM(M là trung điểm của BC)
\(\widehat{BMD}=\widehat{CME}\)(hai góc đối đỉnh)
MD=ME(gt)
Do đó: ΔBMD=ΔCME(c-g-c)
b) Ta có: ΔBMD=ΔCME(cmt)
nên BD=CE(hai cạnh tương ứng)
c) Ta có: ΔBMD=ΔCME(cmt)
nên \(\widehat{BDM}=\widehat{CEM}\)(hai góc tương ứng)
mà \(\widehat{BDM}\) và \(\widehat{CEM}\) là hai góc ở vị trí so le trong
nên BD//EC(Dấu hiệu nhận biết hai đường thẳng song song)
Ta có: BD//EC(cmt)
BD\(\perp\)AB(gt)
Do đó: EC\(\perp\)AB(Định lí 2 từ vuông góc tới song song)

a: Xét ΔBDM và ΔCEM có
MB=MC
\(\widehat{BMD}=\widehat{CME}\)
MD=ME
Do đó: ΔBDM=ΔCEM
b: Xét tứ giác EBDC có
M là trung điểm của ED
M là trung điểm của BC
Do đó: EBDC là hình bình hành
Suy ra: CE//BD
hay CE⊥AB
\(a,\left\{{}\begin{matrix}BM=MC\\ME=MD\\\widehat{BMD}=\widehat{CME}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta BDM=\Delta CEM\left(c.g.c\right)\\ b,\Delta BDM=\Delta CEM\\ \Rightarrow\widehat{BDM}=\widehat{CEM}\\ \text{mà 2 góc này ở vị trí slt nên }CE\text{//}BD\\ \text{Mà }BD\bot AB\Rightarrow CE\bot AB\)


Giúp mình bài này với bạn!!!
http://olm.vn/hoi-dap/question/213159.html