Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a:
Gọi O là trung điểm của CI
Xét tứ giác CKIH có
\(\widehat{CKI}+\widehat{CHI}=90^0+90^0=180^0\)
=>CKIH là tứ giác nội tiếp đường tròn đường kính CI
=>C,K,H,I cùng thuộc (O)
b: Xét (O) có
OI là bán kính
AB\(\perp\)OI tại I
Do đó; AB là tiếp tuyến của (O)
c: Ta có: ΔOKI cân tại O
mà OE là đường cao
nên OE là phân giác của góc KOI
Xét ΔOKE và ΔOIE có
OK=OI
\(\widehat{KOE}=\widehat{IOE}\)
OE chung
Do đó: ΔOKE=ΔOIE
=>\(\widehat{OKE}=\widehat{OIE}\)
=>\(\widehat{OKE}=90^0\)
=>EK là tiếp tuyến của (O)
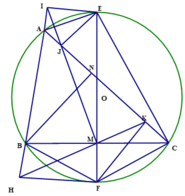
b) Ta có I E M ⏜ = A E C ⏜ ⇒ A E I ⏜ = C E M ⏜ .
Mặt khác A E I ⏜ = A J I ⏜ ( cùng chắn cung IJ), C E M ⏜ = C J M ⏜ ( cùng chắn cung CM). Suy ra C J M ⏜ = A J I ⏜ . Mà I, M nằm hai phía của đường thẳng AC nên C J M ⏜ = A J I ⏜ đối đỉnh suy ra I, J, M thẳng hàng.
Tương tự, ta chứng minh được H, M, K thẳng hàng.
Do tứ giác CFMK nội tiếp nên C F K ⏜ = C M K ⏜ .
Do tứ giác CMJE nội tiếp nên J M E ⏜ = J C E ⏜ .
Mặt khác E C F ⏜ = 90 0 ⇒ C F K ⏜ = J C E ⏜ ( vì cùng phụ với A C F ⏜ ).
Do đó C M K ⏜ = J M E ⏜ ⇒ J M K ⏜ = E M C ⏜ = 90 0 hay I J ⊥ H K
a) Ta có: A I E ^ = A J E ^ = 90 0 nên tứ giác AIEJ nội tiếp.
E M C ^ = E J C ^ = 90 0 nên tứ giác CMJE nội tiếp.
Xét tam giác Δ A E C v à Δ I E M , có
A C E ⏜ = E M I ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác CMJE).
E A C ⏜ = E I M ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác AIEJ).
Do đó hai tam giác Δ A E C ~ Δ I E M đồng dạng
⇒ A E E I = E C E M ⇒ E A . E M = E C . E I (đpcm)
1: AB^2=BH*BC
=>BC=8^2/5=12,8(cm)
\(AC=\sqrt{BC^2-AB^2}=\dfrac{8\sqrt{39}}{5}\left(cm\right)\)
2:
a: Xét tứ giác AMHN có
góc AMH+góc ANH=90+90=180 độ
=>AMHN nội tiếp đường tròn đường kính AH
b: ΔHAC vuông tại H có HM là trung tuyến
nên AC=2HM
Xét ΔABC vuông tại A có AH là đường cao
nên CH*CB=CA^2
=>CH*CB=4HM^2
3: Xét ΔMAN vuông tại A và ΔMHN vuông tại H có
MN chung
MA=MH
=>ΔMAN=ΔMHN
=>AN=HN
=>góc NAH=góc NHA
góc NHA+góc NHB=90 độ
góc NAH+góc NBH=90 độ
mà góc NAH=góc NHA
nên góc NBH=góc NHB
=>NH=NB=NA
=>N là trung điểm của AB
Bạn thịnh ơi bạn có cái hình không ạ
nếu có thì chụp cho mình với
