Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có góc BEC = góc BDC = 90o (góc nội tiếp chắn giữa đường tròn)
Suy ra BD \(\perp\) AC và CE \(\perp\) AB. Mà BD cắt CE tại H là trực tâm \(\Delta\) ABC.
Suy ra AH \(\perp\) BC
Vì AH \(\perp\) BC, BD \(\perp\) AC nên góc HFC = góc HDC = 90o.
Suy ra góc HFC + góc HDC = 180o
Suy ra HFCD là tứ giác nội tiếp
\(\Rightarrow\) góc HDC = góc HCD.
b) Vì M là trung điểm cạnh huyền của hình tam giác vuông ADH nên MD = MA = MH. Tương tự ta có ME = MA = MH
Suy ra MD = ME
Mà OD = OE nên \(\Delta\) OEM = \(\Delta\) ODM \(\Rightarrow\) góc MOE = góc MOD = \(\frac{1}{2}\) góc EOD
Theo qua hệ giữa góc nội tiếp và góc ở tâm cùng chắn cung, ta có góc ECD = \(\frac{1}{2}\) góc EOD
Theo ý a) ta có góc HFD = góc HCD = góc ECD
\(\Rightarrow\) góc MOD = góc HFD hay góc MOD = góc MFD
Suy ra tứ giác MFOD là tứ giác nội tiếp
\(\Rightarrow\) góc MDO = 180o - góc MPO = 90o \(\Rightarrow\) MD \(\perp\) DO
Chứng minh tương tự ta có MEFO là tứ giác nội tiếp
Suy ra 5 điểm M, E, F, O, D cùng thộc 1 đường tròn.

a: Xét (O) có
góc BEC, góc BDC đều là các góc nội tiếp chắn nửa đường tròn
=>góc BEC=góc BDC=90 độ
=>CE vuông góc AB, BD vuông góc AC
Xét ΔABC có
CE,BD là đường cao
CE cắt BD tại H
=>H là trực tâm
=>AH vuông góc BC tại F
góc BEH+góc BFH=180 độ
=>BEHF nội tiếp
b: Xét ΔHCB có CO/CB=CM/CH
nên OM//BH
=>góc COM=góc CBH
=>góc COM=góc FEC
=>góc MOF+góc FEM=180 độ
=>OMEF nội tiếp

a) Xét tứ giác HMBI có:
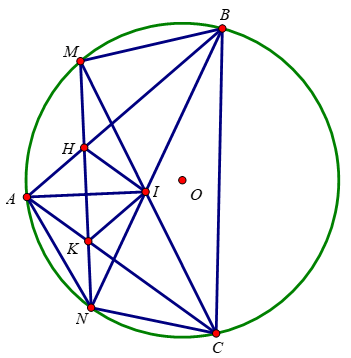
∠HMI = ∠HBI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AN}=\widebat{CN}\))
Mà 2 góc này cùng nhìn cạnh HI
=> Tứ giác BMHI nội tiếp
b) Xét ΔMNI và ΔMKC có:
∠KMC là góc chung
∠MNI = ∠KCM (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{BM}\))
=> ΔMNI ∼ ΔMCK => \(\frac{MN}{MC}=\frac{MI}{MK}\) => MN.MK = MC.MI
c) Xét tứ giác NKIC có:
∠KNI = ∠KCI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{MB}\))
Mà 2 góc này cùng nhìn cạnh KI
=> Tứ giác NKIC là tứ giác nội tiếp
=> ∠NKI + ∠NCI = 180o (1)
Xét đường tròn (O) có:
\(\hept{\begin{cases}\widehat{ANK}=\widehat{ACM}\left(\text{2 góc nội tiếp cùng chắn cung AM}\right)\\\widehat{NAK}=\widehat{NCA}\left(\text{2 góc nội tiếp cùng chắn 2 cung BẰNG NHAU}\widebat{AN}=\widebat{CN}\right)\end{cases}}\)
=> ∠ANK + ∠NAK = ∠ACM + ∠NCA = ∠NCI (2)
Xét tam giác AKN có: ∠ANK + ∠NAK + ∠NKA = 180o (3)
Từ (1), (2), (3) => ∠NKI = ∠NKA
Xét tam giác IKN và tam giác AKN có:
∠NKI = ∠NKA
KN là cạnh chung
∠KNI = ∠KNA (2 góc nội tiếp chắn 2 cung bằng nhau)
=> ΔIKN = ΔAKN
=> IK=AK =>ΔAKI cân tại K
Tứ giác NKIC là tứ giác nội tiếp
Mặt khác ∠KCN = ∠ABN (2 góc nội tiếp cùng chắn cung AN của (O))
∠BAC = ∠BNC (2 góc nội tiếp cùng chắc cung BC của (O))
=> Tứ giác AHIK là hình bình hành
Mà IK = AK
=> Tứ giác AHIK là hình thoi.
CÒN LẠI TỰ LÀM LÀM NHA

\(\text{a) Xét tứ giác BEFC có:}\)
\(\text{∠BEC = 90 o (CE là đường cao)}\)
\(\text{∠BFC = 90 ^0 (BF là đường cao)}\)
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc vuông
=> Tứ giác BEFC là tứ giác nội tiếp
\(\text{Xét tứ giác AEHF có:}\)
\(\text{∠AEH = 90 o (CE là đường cao)}\)
\(\text{∠AFH = 90 o (BF là đường cao)}\)
=> ∠AEH + ∠AFH = 180^ o
=> Tứ giác AEHF là tứ giác nội tiếp.
\(\text{b) Xét ΔSBE và ΔSFC có:}\)
\(\text{∠FSC là góc chung}\)
\(\text{∠SEB = ∠SCF (Tứ giác BEFC là tứ giác nội tiếp)}\)
=> ΔSBE ∼ ΔSFC (g.g)
\(\Rightarrow\frac{SB}{SF}\)=\(\frac{SE}{SC}\)\(\Rightarrow\text{SE.SF = SB.SC (1)}\)
\(\text{Xét ΔSMC và ΔSNB có:}\)
\(\text{∠ NSC là góc chung}\)
\(\text{∠ SCM = ∠SNB (Hai góc nội tiếp cùng chắn cung MB)}\)
=> ΔSMC ∼ ΔSBN (g.g)
\(\Rightarrow\frac{SM}{SB}\)=\(\frac{SC}{SN}\Rightarrow\text{SM.SN = SB.SC (2)}\)
Từ (1) và (2) => SE.SF = SM.SN
\(\text{c) Ta có:}\)
\(\hept{\begin{cases}\widehat{KAE}=\widehat{KCB}\left(\text{2 GÓC NỘI TIẾP CÙNG CHẮN CUNG KB}\right)\\\widehat{HAE}=\widehat{BFM}\left(\text{TỨ GIÁC AEHF LÀ TỨ GIÁC NỘI TIẾP}\right)\\\widehat{KCB}=\widehat{BFM}\left(\text{TỨ GIÁC BEFC LÀ TỨ GIÁC NỘI TIẾP}\right)\end{cases}}\)
=> ∠KAE = ∠HAE
=> AE là tia phân giác của góc ∠KAH
\(\text{Mà AE cũng là đường cao của tam giác KAH}\)
=> ΔKAH cân tại A
=> AE là đường trung tuyến của ΔKAH
=> E là trung điểm của KH hay K và H đối xứng nhau qua AB
\(\text{d) Tia BF cắt đường tròn (O) tại J}\)
∠KJB = ∠KCB (2 góc nội tiếp cùng chắn cung KB)
∠KCB = ∠EFH (tứ giác BEFC là tứ giác nội tiếp )
=> ∠KJB = ∠EFH
Mà 2 góc này ở vị trí so le trong
=> KJ // EF
KI // EF (gt)
=> I ≡ J
=> H, F, J thẳng hàng
HÌNH THÌ VÀO XEM THỐNG KÊ HỎI ĐÁP NHA
BÀI LÀM ĐÚNG MÀ SAO CÓ NGƯỜI K SAI TÔI ĐẢM BẢO BÀI NÀY ĐÚNG 100%

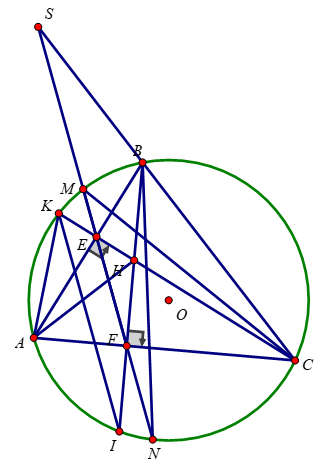
\(\text{a) Ta có:}\)
∠BFC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AFC = 90o
∠BEC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AEC = 90o
Tứ giác AEHF có:
∠AFC = 90o
∠AEC = 90o
=>∠AFC + ∠AEC = 180o
=> AEHF là tứ giác nội tiếp
b) ∠AFH = 90o => AH là đường kính đường tròn ngoại tiếp tứ giác AEHF
\(\text{Do đó trung điểm I của AH là tâm đường tròn ngoại tiếp tứ giác AEHF}\)
=> Bán kính đường tròn ngoại tiếp tứ giác AEHF là R = AI = \(\frac{AH}{2}\) = 2cm
Ta có: ∠BAC = 60o
=> ∠FIE = 2∠BAC = 120o (Góc nội tiếp bằng \(\frac{1}{2}\) góc ở tâm cùng chắn một cung)
=> Số đo ∠EHF = 120o
Diện tích hình quạt IEHF là:
\(S=\frac{\pi R^2N}{360}=\frac{\pi.2^2.120}{360}=\frac{4\pi}{3}\left(ĐVDT\right)\)
\(\text{c) Xét tam giác ABC có: }\)
BE và CF là các đường cao
BE giao với CF tại H
=> H là trực tâm tam giác ABC
=>AH ⊥ BC hay ∠ADC = ∠ADB = 90o
Xét tứ giác BEFC có:
∠BFC = ∠BEC = 90o
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc bằng nhau
=> BEFC là tứ giác nội tiếp
=> ∠HFE = ∠BEC ( 2 góc nội tiếp cùng chắn cung EC) (1)
Xét tứ giác BFHD có:
∠BFH = ∠HDB = 90o
=>∠BFH + ∠HDB = 180o
=> Tứ giác BFHD là tứ giác nội tiếp ( tổng 2 góc đối bằng 180o)
=> ∠DFH = ∠BEC ( 2 góc nội tiếp cùng chắn cung HD) (2)
Từ (1) và (2) = > ∠HFE = ∠DFH
=> FH tia phân giác của góc ∠DFE
d) Tam giác OFB cân tại O => ∠OFB = ∠FBO
Tam giác BFC vuông tại F => ∠FBO + ∠HCD = 90o
=> ∠OFB + ∠HCD = 90o (*)
\(\hept{\begin{cases}\Delta FIH\text{CÂN TẠI I}\\\widehat{IHF}=\widehat{DHC}\left(\text{ĐỐI ĐỈNH}\right)\\\Delta HDC\text{VUÔNG TẠI D}\Rightarrow\widehat{DHC}+\widehat{HDC}=90^0\end{cases}}\Rightarrow\widehat{IFH}+\widehat{HDC}=90^0\)
Từ (*) và (**) => ∠OFB = ∠IFH
=> ∠OFB + ∠OFH = ∠IFH + ∠OFH <=> ∠BFC = ∠FIO <=> ∠FIO) = 90o
Vậy FI là tiếp tuyến của (O)
Chứng minh tương tự EI là tiếp tuyến của (O)
Mà I là trung điểm của AH
=> Tiếp tuyến của (O) tại E và F và AH đồng quy tại 1 điểm.
HÌNH THÌ VÀO THỐNG KÊ HỎI ĐÁP CỦA MIK NHA
VCN JACK trả lời cuc64 kì đ luôn . đ là chất

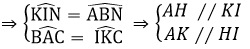
Chỉ lm bài thoii, hình bn tự vẽ nha !!!
\(a.\) Tứ giác \(BEDC\) có \(\widehat{BEC}=\widehat{BDC}=90^0\)
Suy ra tứ giác \(BEDC\) là tứ giác nội tiếp
Tam giác \(DBA\) vuông tại \(D\) có đường cao \(DL\) nên suy ra \(BD^2=BL.BA\)
\(b.\) Tứ giác \(ADEH\) có:
\(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\) nên tứ giác \(ADEH\) nội tiếp
Từ đó \(\widehat{BAK}=\widehat{BDE}\)
Mà \(\widehat{BJK}=\widehat{BAK}\) ( 2 góc nội tiếp cùng chắn một cung )
Do đó \(\widehat{BJK}=\widehat{BDE}\)
Câu c mk làm sau cho nha !