Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Nửa mặt phẳng chứa M và nửa mặt phẳng chứa N,P là hai nửa mặt phẳng bờ a đối nhau
b.
Đoạn thẳng MN cắt aa nên M và N thuộc hai mặt phẳng đối nhau có bờ là a
Đoạn thẳng MP cắt aa nên M và P thuộc hai mặt phẳng đối nhau có bờ là a
→A và Ccùng thuộc một nửa mặt phẳng có bờ là a
→ Đoạn thẳng NP không cắt đường thẳng a

a. Nửa mặt phẳng chứa M và nửa mặt phẳng chứa N,P là hai nửa mặt phẳng bờ a đối nhau
b.
Đoạn thẳng MN cắt a nên M và N thuộc hai mặt phẳng đối nhau có bờ là a
Đoạn thẳng MP cắt a nên M và P thuộc hai mặt phẳng đối nhau có bờ là a
→A và C cùng thuộc một nửa mặt phẳng có bờ là a
→ Đoạn thẳng NP không cắt đường thẳng a

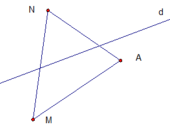
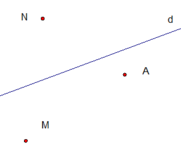
a/ Gọi tên hai nửa mặt phẳng đối nhau bờ d là nửa mặt phẳng bờ d chứa điểm N và nửa mặt phẳng bờ d chứa điểm A
b/ Vẽ các đoạn thẳng AM, AN, MN
c/ Đường thẳng d cắt cạnh AN, MN của tam giác AMN
d/ d không cắt cạnh AM vì A và M cùng nằm trên 1 nửa mặt phẳng bờ d

1.Ta có :\(P=\frac{-n+2}{n-1}=\frac{-n+1+1}{n-1}=-1+\frac{1}{n-1}\)
Để\(P\in Z\)thì\(\frac{1}{n-1}\in Z\Rightarrow1⋮n-1\)=> n - 1 = -1 ; 1 => n = 0 ; 2
2.Ta có :\(M=\frac{6n-3}{4n-6}=\frac{3\left(2n-3\right)+6}{2\left(2n-3\right)}=\frac{3}{2}+\frac{3}{2n-3}\)
Để M lớn nhất thì\(\frac{3}{2n-3}\)lớn nhất => 2n - 3 nguyên dương và nhỏ nhất,tức 2n - 3 = 1 => n = 2
Vậy n = 2 thì M đạt giá trị lớn nhất là :\(\frac{3}{2}+\frac{3}{1}=\frac{9}{2}\)
3.a) TH1 : A nằm cùng phía với B,C thì trên cùng tia Ax (hay Ay),ta có AB < AC ( a < b) nên B nằm giữa A và C.Suy ra :
- AB + BC = AC => BC = AC - AB = b - a
- 2 tia BA,BC đối nhau mà 2 tia BI,BA trùng nhau (vì I thuộc đoạn AB) nên 2 tia BI,BC đối nhau => B nằm giữa I,C
=> IC = BI + BC mà BI =\(\frac{AB}{2}=\frac{a}{2}\)(I là trung điểm AB) nên IC =\(\frac{a}{2}+b-a=b-\frac{a}{2}\)
TH2 : A nằm khác phía với B,C hay A nằm giữa B,C thì 2 tia AB,AC đối nhau mà AI,AB trùng nhau (vì I thuộc đoạn AB)
=> 2 tia AI,AC đối nhau => A nằm giữa I,C => IC = IA + AC mà IA =\(\frac{AB}{2}=\frac{a}{2}\)(I là trung điểm AB) => IC =\(\frac{a}{2}+b\)
b) Ta có 3 trường hợp :
TH1 : Cả 4 điểm đều nằm trên 1 nửa mặt phẳng bờ xy thì xy không cắt đoạn nào trong 6 đoạn trên
TH2 : 1 điểm và 3 điểm còn lại nằm trên 2 nửa mặt phẳng đối nhau bờ xy.Ví dụ điểm M và 3 điểm N,P,Q thì xy cắt 3 đoạn : MN,MP,MQ
TH3 : 2 điểm và 2 điểm còn lại nằm trên 2 nửa mặt phẳng đối nhau bờ xy.Ví dụ điểm M,N và điểm P,Q thì xy cắt 4 đoạn : MP,MQ,NP,NQ
Đúng không đây để mình chép với, cô mình cũng ra đề như thế này nè!