Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét tam giác MNP có:
D là trung điểm MN
DE//NP
E thuộc MP
=> E là trung điểm MP
b) Xét tam giác MNP có:
D là trung điểm MN
E là trung điểm MP
=> DE là đường trung bình
\(\Rightarrow DE=\dfrac{1}{2}NP=\dfrac{1}{2}.6=3\left(cm\right)\)
a: Xét ΔPMN có
F,E lần lượt là trung điểm của PM,PN
=>FE là đường trung bình của ΔPMN
=>FE//MN và \(FE=\dfrac{MN}{2}\)
Ta có: FE//MN
D\(\in\)MN
Do đó: FE//MD
Ta có: \(FE=\dfrac{MN}{2}\)
\(MD=DN=\dfrac{MN}{2}\)
Do đó: FE=MD=ND
Xét tứ giác MDEF có
FE//MD
FE=MD
Do đó: MDEF là hình bình hành
Hình bình hành MDEF có \(\widehat{FMD}=90^0\)
nên MDEF là hình chữ nhật
b: ta có: FE//MN
D\(\in\)MN
Do đó: FE//DN
Xét tứ giác NDFE có
FE//ND
FE=ND
Do đó: NDFE là hình bình hành
=>NF cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của NF
=>N,I,F thẳng hàng
Bạn xem lời giải tại đây:
https://hoc24.vn/cau-hoi/cho-tam-giac-mnp-vuong-tai-m-co-d-e-f-lan-luot-la-trung-diem-cua-mn-np-mpa-tu-giac-mdef-la-hinh-gi-vi-saob-goi-i-la-trung-diem-cua-de-chung-minh-3-diem-n-i-f-thang-hangc-chung-minh-if.8722192330796
Lời giải:
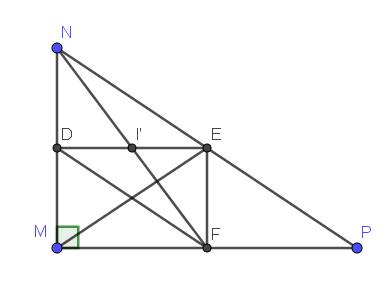
a. $D,E,F$ là trung điểm $MN,NP,MP$ nên $EF, DE$ lần lượt là đường trung bình của tam giác $ABC$ ứng với lần lượt 2 cạnh $MN, MP$
$\Rightarrow EF\parallel MN, DE\parallel MP$
Mà $MN\perp MP$ nên $EF\perp MP, DE\perp MN$
$\Rightarrow \widehat{EFM}=\widehat{EDM}=90^0$
Tứ giác $MDEF$ có 3 góc vuông $\widehat{M}=\widehat{D}=\widehat{F}$ nên là hình chữ nhật.
b.
Gọi $I'$ là giao điểm $NF$ và $DE$
Do $DE\parallel MP$ nên $DI'\parallel MF$
Áp dụng định lý Talet:
$\frac{DI'}{MF}=\frac{ND}{NM}=\frac{1}{2}$
$\Rightarrow MF=2DI'$
Mà $MF=DE$ (do $MFED$ là hcn)
$\Rightarrow DE=2DI'$
$\Rightarrow I'$ là trung điểm của $DE$
$\Rightarrow I\equiv I'$
Mà $I', N, F$ thẳng hàng nên $I, N, F$ thẳng hàng.
c.
Có: $\frac{NI}{NF}=\frac{ND}{NM}=\frac{1}{2}$ nên $I$ là trung điểm $NF$
$DF$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow DF=\frac{1}{2}NP\Rightarrow ME=DF=\frac{1}{2}NP$.
Khi đó ta có:
$NF.ME-IF.PE = 2IF.\frac{1}{2}NP-IF.PE$
$=IF.NP-IF.PE = IF(NP-PE) = IF.NE$
a: Xét ΔMNP có
D là trung điểm của MP
E là trung điểm của MN
Do đó: DE là đường trung bình của ΔMNP
Suy ra: DE//NP
hay PDEN là hình thang vuông
DE=NP/2=11(cm)
Sửa đề: DE vuông góc với MP tại F
a) Xét tứ giác MEDF có
\(\widehat{EMF}=90^0\)(\(\widehat{NMP}=90^0\), E∈MN, F∈MP)
\(\widehat{DEM}=90^0\)(DE⊥MN)
\(\widehat{DFM}=90^0\)(DF⊥MP)
Do đó: MEDF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
a ) Xét ◇DENF có :
Góc N = Góc F = Ê = 90°
\(\Rightarrow\)◇DENF là hình chữ nhật
b ) Trong \(\Delta\)MNP có : ND là đường trung tuyến
\(\Rightarrow\)ND = DP ( vì đường trung tuyến bằng nữa cạnh huyền )
Xét \(\Delta\)NDF và \(\Delta\)PDF có :
- ND = DP ( cmt )
- Góc NFD = Góc PFD ( = 90° )
- DF : cạnh chung
\(\Rightarrow\)\(\Delta\)NDF = \(\Delta\)PDF ( cạnh huyền - cạnh góc vuông )
\(\Rightarrow\)NF = PF ( 2 cạnh tương ứng )
\(\Rightarrow\)F là trung điểm NP
a) Xét tứ giác NEDF có +) \(\widehat{ENF}=90^0\)(tam giác MNP vuông tại N)
+) \(\widehat{DFN}=90^0\)(DF vuông góc NP)
+) \(\widehat{DEN}=90^0\)(DE vuông góc MN)
\(\Rightarrow\)tứ giác NEDF là hình chữ nhật
b) Xét \(\Delta DFN\)và \(\Delta DFP\)có:
DF : cạnh chung
DN = DP ( Do ND là trung tuyến của tam giác vuông MNP)
Do đó \(\Delta DFN\)\(=\Delta DFP\left(ch-cgv\right)\)
\(\Rightarrow NF=PF\)
Suy ra F là trung điểm của NP (đpcm)
a, Vì \(\widehat{KMH}=\widehat{KHD}=\widehat{KMD}=90^0\) nên MHDK là hcn
b, Vì \(PD=DN;DH//PM\left(\perp MN\right)\) nên \(MH=HN\)
Vì \(PD=DN;DK//MN\left(\perp PM\right)\) nên \(PK=KM\)
Tứ giác MDNE có H là trung điểm MN;DE và \(MN\perp DE\) tại H nên là hthoi
Tứ giác MDPF có K là trung điểm PM;DF và \(MP\perp DF\) tại K nên là hthoi
c, Vì MDNE và MDPF là hình thoi nên MF//PD;ME//DN
Mà PD trùng PN nên ME trùng MF hay M;F;E thẳng hàng
Vì MDNE và MDPF là hình thoi nên \(MF=PD;ME=DN\)
Mà \(PD=DN\) nên \(MF=ME\)
Vậy E đx F qua M
a: Xét ΔQMD có
N là trung điểm của MQ
I là trung điểm của MD
Do đó: NI là đường trung bình của ΔQMD
a: Xét ΔDNP có
D là trung điểm của MN
DE//NP
Do đó: E là trung điểm của MP
b: Xét ΔDNP có
D là trung điểm của MN
E là trung điểm của MP
Do đó: DE là đường trung bình của ΔDNP
Suy ra: \(DE=\dfrac{NP}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Ta có: DE//NP
PN=PN
→DE là đường trung bình của tam giác MNP
a)→E là trung điểm của NP
DE=NP/2
=6/2
=3cm