Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: AH^2=HB*HC
=>AH/HB=HC/HA
=>ΔAHC đồng dạng với ΔBHA
=>góc HAC=góc HBA
=>góc HAC+góc HAB=90 độ
=>góc BAC=90 độ
Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật

Xét ΔABH vuông tại H(gt)
=> \(AH^2=AE\cdot AB\) (1)
Xét ΔAHC vuông tại C(gt)
=>\(AH^2=AF\cdot AC\) (2)
Từ (1)(2) suy ra:
AE.AB=AF.AC
b) Xét ΔABH vuông tại H(gt)
=> \(AB^2=AH^2+BH^2=3^2+4^2=9+16=25\)
=>AB=25
Áp dụng hệ thức ta có:
\(AH^2=AE\cdot AB\)
=> \(AE=\frac{AH^2}{AB}=\frac{4^2}{5}=\frac{16}{5}\)
Có: AB=AE+BE
=>BE=AB-AE= \(5-\frac{16}{5}=\frac{9}{5}\)

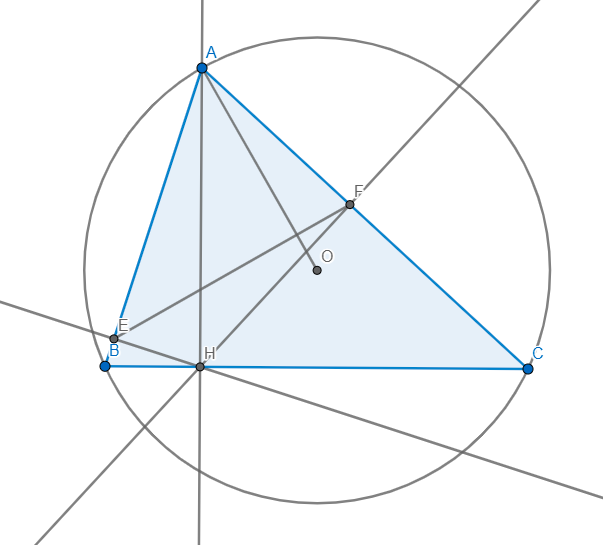
a) Ta có: \(\angle AEH+\angle AFH=90+90=180\Rightarrow AEHF\) nội tiếp
b) AEHF nội tiếp \(\Rightarrow\angle EFA=\angle EHA=90-\angle BHE=\angle ABC\)
c) Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle OAC+\angle ABC=90\Rightarrow\angle OAC+\angle AFE=90\Rightarrow OA\bot EF\)

b: AH^2=HB*HC
=>AH/HB=HC/HA
=>ΔAHC đồng dạng với ΔBHA
=>góc HAC=góc HBA
=>góc HAC+góc HAB=90 độ
=>góc BAC=90 độ
Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật