Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là trung điểm của BC
Xét ΔABC có AM là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AM}\)
\(\Leftrightarrow\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=a\)

A B C
a) \(\overrightarrow{AB}.\overrightarrow{AC}=0\) do \(AB\perp AC\).
b)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{a^2+a^2}=\sqrt{2}a\).
\(\overrightarrow{BA}.\overrightarrow{BC}=BA.BC.cos\left(\overrightarrow{BA},\overrightarrow{BC}\right)=a.\sqrt{2}a.cos45^o=a^2\).
c) \(\overrightarrow{AB}.\overrightarrow{BC}=-\overrightarrow{BA}.\overrightarrow{BC}=-a^2\).

a) Có \(\overrightarrow{BC}^2=\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2=\overrightarrow{AC}^2+\overrightarrow{AB}^2-2\overrightarrow{AC}.\overrightarrow{AB}\)
Suy ra: \(\overrightarrow{AC}.\overrightarrow{AB}=\dfrac{\overrightarrow{AC^2}+\overrightarrow{AB}^2-\overrightarrow{BC}^2}{2}=\dfrac{8^2+6^2-11^2}{2}=-\dfrac{21}{2}\).
Do \(\overrightarrow{AC}.\overrightarrow{AB}< 0\) nên \(cos\widehat{BAC}< 0\) suy ra góc A là góc tù.
b) Từ câu a suy ra: \(cos\widehat{BAC}=\dfrac{\overrightarrow{AB}.\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|}=-\dfrac{21}{2.6.8}=-\dfrac{7}{32}\).
Do N là trung điểm của AC nên \(AN=AC:2=8:2=4cm\).
\(\overrightarrow{AM}.\overrightarrow{AN}=AM.AN.cos\left(\overrightarrow{AM},\overrightarrow{AN}\right)\)
\(=2.4.cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=2.4.\dfrac{-7}{32}=-\dfrac{7}{4}\).
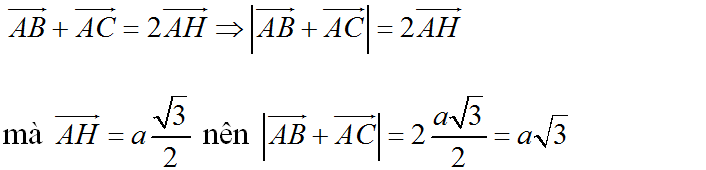



A B C a
a) \(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=a.a.cos60^o=a.a.\dfrac{1}{2}\)\(=\dfrac{a^2}{2}\).
\(\overrightarrow{AB}.\overrightarrow{BC}=-\overrightarrow{BA}.\overrightarrow{BC}==-a.a.cos\left(\overrightarrow{BA},\overrightarrow{BC}\right)\)\(=-a.a.cos60^o=-\dfrac{a^2}{2}\).
\(\overrightarrow{AB}.\overrightarrow{AC}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|.cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=a.a.cos60=\dfrac{1}{2}a^2\)\(\overrightarrow{AB}.\overrightarrow{BC}=-\overrightarrow{BA}.\overrightarrow{BC}=-\left(\overrightarrow{BA}.\overrightarrow{BC}\right)=-\left(\left|\overrightarrow{BA}\right|.\left|\overrightarrow{BC}\right|.cos\left(\overrightarrow{BA},\overrightarrow{BC}\right)\right)=-\left(a.a.cos60\right)=-\dfrac{1}{2}a^2\)