Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có ΔEDF cân ở D =>DE=DF; góc E =góc F
xét ΔDEM và ΔDFM có
DM là trung tuyến => EM=FM
góc E =góc F (cmt)
DE=DF (cmt)
=>ΔDEM = ΔDFM (cgc)
b)Có Δ DEF cân mà DM là trung tuyến
=> DM là đường cao (tc Δ cân )
=> DM⊥EF
c) EM=FM=EF/2=5
xét ΔDEM có DM ⊥ EF => góc EMD =90o
=>EM2+DM2=ED2 (đl pitago)
=>52+DM2=132 => DM=12
d) Ta có G là trọng tâm của ΔDEF
=>DG=2/3DM=> DG=2/3*12=8

I là trung điểm của EF nên IE = IF = EF/2 = 5cm.
Ta có : 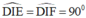 ⇒ ΔDIE vuông tại I
⇒ ΔDIE vuông tại I
Theo định lý Pitago trong tam giác vuông DIE ta có :
DE2 = DI2 + EI2 ⇒ DI2 = DE2 – EI2 = 132 – 52 = 144 ⇒ DI = 12 (cm).

a)Xét\(\Delta DEF\)có:\(EF^2=DE^2+DF^2\)(Định lý Py-ta-go)
hay\(5^2=3^2+DF^2\)
\(\Rightarrow DF^2=5^2-3^2=25-9=16\)
\(\Rightarrow DF=\sqrt{16}=4\left(cm\right)\)
Ta có:\(DE=3cm\)
\(DF=4cm\)
\(EF=5cm\)
\(\Rightarrow DE< DF< EF\)hay\(3< 4< 5\)
b)Xét\(\Delta DEF\)và\(\Delta DKF\)có:
\(DE=DK\)(\(D\)là trung điểm của\(EK\))
\(\widehat{EDF}=\widehat{KDF}\left(=90^o\right)\)
\(DF\)là cạnh chung
Do đó:\(\Delta DEF=\Delta DKF\)(c-g-c)
\(\Rightarrow EF=KF\)(2 cạnh t/ứ)
Xét\(\Delta KEF\)có:\(EF=KF\left(cmt\right)\)
Do đó:\(\Delta KEF\)cân tại\(F\)(Định nghĩa\(\Delta\)cân)
c)Ta có:\(DF\)cắt\(EK\)tại\(D\)là trung điểm của\(EK\Rightarrow DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)cắt\(EF\)tại\(I\)là trung điểm của\(EF\Rightarrow KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
Ta lại có:\(DF\)cắt\(KI\)tại\(G\)
mà\(DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
\(\Rightarrow G\)là trọng tâm của\(\Delta KEF\)
\(\Rightarrow GF=\frac{2}{3}DF\)(Định lí về TC của 3 đg trung tuyến của 1\(\Delta\))
\(=\frac{2}{3}.4=\frac{8}{3}\approx2,7\left(cm\right)\)
Vậy\(GF\approx2,7cm\)

a) Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(EF^2=DE^2+DF^2\)
\(\Leftrightarrow EF^2=9^2+12^2=225\)
hay EF=15(cm)
Vậy: EF=15cm

A) Xét tam giác DEI và tam giac DFI
DE=DF
DI chung
IE=IF
\(\Rightarrow\)2 tam giác đó = nhau
b)Từ 2 tam giác trên = nhau suy ra \(\widehat{DIE}\)=\(\widehat{DI}F\)
Mà \(\widehat{DIE}\)+\(\widehat{DIF}\)=180 độ
Suy ra 2 góc đó = nhau và bằng 90 độ

a) Xét \(\Delta\)DEM và \(\Delta\)DFM có:
DM chung
\(E\widehat{D}M=F\widehat{D}M\left(Vì.DM.là.phân.giác.của.E\widehat{D}F\right)\)
DE=DF(giả thiết)
\(\Rightarrow\Delta=\Delta\left(c.g.c\right)\)
b)Chịu:)
c)Ta có \(\Delta DEM=\Delta DFM\left(cmt\right)\)
=>ME=MF(2 góc tương ứng)
=>M là trung điểm của FE
EF=căn 3^2+4^2=5cm
DM=5/2=2,5cm