Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1, Xét \(\Delta MNP\) cân tại \(M\) có
\(\widehat{N}=\widehat{D}=\dfrac{180^o-\widehat{M}}{2}=\dfrac{180^o-70^o}{2}=55^o\)
2, Xét \(\Delta DEF\) cân tại \(D\)
\(\Rightarrow\widehat{E}=\widehat{F}=40^o\) ( hai góc đáy bằng nhau )
Ta có tổng 3 góc trong tam giác
\(\widehat{D}+\widehat{E}+\widehat{F}=180^o\\ =>\widehat{D}=180^o-40^o-40^o=100^o\)
1: góc N=góc P=(180-70)/2=55 độ
2: góc F=góc E=40 độ
góc D=180-40*2=100 độ

Ta có: tam giác DEF = tam giác HIK
=> DE = HI ; EF = IK ; DF = HK
=> góc D = góc H
góc E = góc I
góc F = góc K
a/ Ta có: góc E = góc I (vì tam giác DEF = HIK)
Mà góc E = 400 => góc I = 400
b/ Chu vi tam giác DEF= chu vi tam giác HIK
= DE + EF + HK = DE+EF+DF=2+5+6=13 (cm)
Vậy chu vi tam giác DEF = chu vi tam giác HIK = 13 cm

Bài 1:
Số đo góc ngoài tại đỉnh C là \(74^0+47^0=121^0\)
Câu 2:
Đặt \(\widehat{D}=a;\widehat{E}=b\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=52\\a+b=140\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=96\\b=44\end{matrix}\right.\)
Bài 3:
Theo đề, ta có: x+2x+3x=180
=>6x=180
=>x=30
=>\(\widehat{A}=30^0;\widehat{B}=60^0;\widehat{C}=90^0\)

Tổng ba góc của một tam giác là 180
vậy góc A=180*2/5 =72 biết \(\frac{1}{2}\)A là 1,E là 2
sau khi biết góc A thì tính góc E; E=180-72=108
Cứ tương tự mà bạn làm tiếp nhé giờ mình phải đi học rồi

Ta có\(\Delta ABC=\Delta DEF\)(1)
=> \(\hept{\begin{cases}AB=DE\\AC=DF\\BC=EF\end{cases}}\)(cạnh tương ứng) => EF = 8 cm
Tư (1) => \(\widehat{A}=\widehat{D}\)(góc tương ứng)
Lại có trong \(\Delta ABC\)có \(\widehat{A}+\widehat{B}+\widehat{C}=180^{\text{o}}\)
=> \(\widehat{A}+70^{\text{o}}+40^{\text{o}}=180^{\text{o}}\)
=> \(\widehat{A}=70^{\text{o}}\)
=> \(\widehat{D}=70^{\text{o}}\)

a: ΔABC và ΔEFD
Để ΔABC=ΔEFD theo trường hợp c-g-c thì BC=FD
b: ΔABC=ΔEFD
nên AB=EF=5cm; AC=ED=6cm; BC=FD=6cm
=>\(C_{ABC}=C_{EFD}=5+6+6=17\left(cm\right)\)

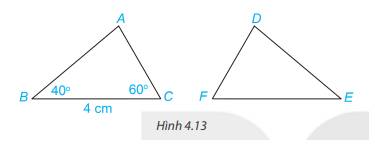
Vì \(\Delta ABC = \Delta DEF\) nên BC = EF ( 2 cạnh tương ứng); \(\widehat A = \widehat {EDF}\) ( 2 góc tương ứng)
Mà BC = 4 cm nên EF = 4 cm
Trong tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) ( định lí tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow \widehat A + 40^\circ + 60^\circ = 180^\circ \\ \Rightarrow \widehat A = 180^\circ - 40^\circ - 60^\circ = 80^\circ \end{array}\)
Mà \(\widehat A = \widehat {EDF}\) nên \(\widehat {EDF} = 80^\circ \)
a,\(=>\angle\left(EDF\right)=180^o-\angle\left(DEF\right)-\angle\left(DFE\right)=80^O\)
b,\(\angle\left(EDM\right)=\angle\left(MDF\right)=\dfrac{\angle\left(EDF\right)}{2}=40^o\)
c,\(\angle\left(DME\right)=\angle\left(DFE\right)+\angle\left(MDF\right)=80^o\)