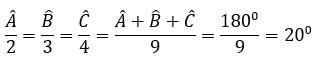Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 3 góc A; B; C lần lượt là x; y; z (x; y; z >0)
Ta có: x + y + z = 1800 (tổng 3 góc trong của tam giác)
Vì x; y; z lần lượt tỉ lệ với 2; 3; 4 => \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y+z}{2+3+4}=\frac{180}{9}=20\)
=> \(\frac{x}{2}=20=>x=20.2=40\)
\(\frac{y}{3}=20=>y=20.3=60\)
\(\frac{z}{4}=20=>z=20.4=80\)
Vậy:
Góc A bằng 400
Góc B bằng 600
Góc C bằng 800

Tam giác ABC có số đo các góc là \widehat{A}A , \widehat{B}B , \widehat{C}C lần lượt tỉ lệ với 2 ; 3 ; 4. Tính số đo các góc của \DeltaΔABC.

gọi số đo 3 góc của tam giác là :A,B,C
theo bài ra ta có:
A:B:C=2:3:4
hay \(\frac{A}{2}=\frac{B}{3}=\frac{C}{4}\) và A+B+C=180độ(vì tổng 3 góc của tam giác =180độ)
áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{A}{2}=\frac{B}{3}=\frac{C}{4}=\frac{A+B+C}{2+3+4}=\frac{180^0}{9}=20\)
--> A=\(20.2=40^0\)
B=\(20.3=60^0\)
C=\(20.4=80^0\)
vậy số đo 3 góc của tam gics lần lượt : \(40^0,60^0,80^0\)
gọi số đo 3 góc là a,b,c ( a,b,c > 0 )
ta có a : b : c = 2 : 3 : 4 và a + b+ c = 180
=> a /2 = b/3= c/4 và a + b + c =180
=> Ap dụng dãy tỉ số = nhau : a/2 = b/3 = c/4 = ( a + b + c ) / ( 2 + 3 + 4 ) = 180 /9 = 20
=> a/2 = 20 => a = 40
=> b/3=20 => b = 60
=> c/4 = 20 => c= 80

1) bạn sai đề rồi phải tỉ lệ với 2;4;5 cơ mik làm rồi hjhj
gọi độ dài các cạnh đó lần lượt là a;b;c
=>a/2=b/4=c/5
áp dug t/c dãy t/s = nhua ta có:
a/2=b/4=c/5=a+b+c/2+4+5=22/11=2
=>a/2=2=>a=4
=>b/4=2=>b=8
=>c/5=2=>c=10

Gọi số do các góc là : x,y,z
Ta có : x : y : z = 2 : 3 : 4
\(\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)
Vì : x,y,z là các góc trong 1 tam giác nên : x + y + z = 180
Ta có : \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y+z}{2+3+4}=\frac{180}{9}=20\)
Nên : \(\frac{x}{2}=20\Rightarrow x=40\)
\(\frac{y}{3}=20\Rightarrow y=60\)
\(\frac{z}{4}=20\Rightarrow z=80\)
Vậy .....................
Gọi 3 góc của tam giác đó là a,b,c
Theo bài ra ta có :
\(a:2\)
\(b:3\)
và \(c:4\)
Và tổng ba góc của tam giác là 180
\(\Rightarrow a+b+c=180^o\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{2}+\frac{b}{3}+\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{180^o}{9}=20^o\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{2}=20^o\\\frac{b}{3}=20^o\\\frac{c}{4}=20^o\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a=40^o\\b=60^o\\c=80^o\end{cases}}\)
Vậy .......