

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




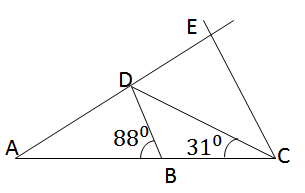
Hình bạn tự vẽ.
Xét \(\Delta ABC\)cân tại A ta có:
\(\widehat{DAC}=180^o-2\widehat{ACD}\)
\(\widehat{DAC}=180^o-2\cdot31^o=118^o\)
Mà \(\widehat{DAC}=\widehat{ABD}+\widehat{ADB}\)( góc ngoài tại đỉnh A của \(\Delta ABD\))
Nên \(118^o=88^o+\widehat{ADB}\)
\(\Rightarrow\)\(\widehat{ADB}=118^o-88^o=30^o\)
Mặt khác \(\widehat{ADB}=\widehat{DEC}\)( 2 góc so le trong và BD // EC )
\(\Rightarrow\)\(\widehat{DEC}=30^o\)
Ta có:
\(\widehat{ACE}=\widehat{ABD}\)( 2 góc so le trong và BD // EC )
\(\widehat{ABD}=88^o\left(gt\right)\)
\(\Rightarrow\)\(\widehat{ACE}=88^o\)
Mà \(\widehat{DCE}=\widehat{ACD}+\widehat{ACE}\)
Nên \(\widehat{DCE}=31^o+88^o=119^o\)
Ta có:
\(\widehat{ACD}=\widehat{ADC}\)( \(\Delta ACD\)cân tại A)
\(\widehat{ACD}=31^o\)
\(\Rightarrow\)\(\widehat{ADC}=31^o\)
Xét \(\Delta ECD\)ta có:
\(\widehat{DCE}>\widehat{EDC}>\widehat{DEC}\left(119^o>31^o>30^o\right)\)
\(\Rightarrow\)\(ED>EC>CD\)( Quan hệ cạnh góc đối diện trong tam giác )
Vậy cạnh \(DE\)lớn nhất trong \(\Delta CDE\)

a, vì CE//AD nên \(\widehat{ECA}\)=\(\widehat{DAB}\)mà \(\widehat{DAB}\)=90 độ -45 độ=45 độ
=> \(\widehat{ECA}\)=45 độ
trong tam giác EAC có: \(\widehat{EAC}\)=90 độ; \(\widehat{ECA}\)=45 độ(1)
=> \(\widehat{AEC}\)=45 độ(2)
từ (1) và (2) suy ra tam giác AEC cân tại A
b, tam giác AEC cân tại A mà có góc A vuông nên tam giác AEC vuông cân
=> EC là cạnh huyền của tam giác vuông AEC nên EC là cạnh lớn nhất(cạnh huyền lớn hơn cạnh góc vuông)
=> A B C D x E