Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác AMB và tam giác CME có :
BM=ME (gt)
Góc AMB = góc CME ( đối đỉnh )
AM = MC ( gt )
-> vậy tam giác AMB = tam giác CME (c.g.c)
b)
a/(c.g.c)
b/ CE=AB ( cặp cạnh tương ứng)
Mà: AB<BC( cạnh huyền lớn nhất)
Nên CE<BC
c/góc ABM=góc CEM(cặp góc tương ứng) (1)
Xét tam giác BCE có: CE<BC( CMT)
Suy ra góc CEM<góc MBC (2) ( Quan hệ giữa góc và cạnh đối diện trong 1 tam giác)
Vậy: từ (1) và (2), ta có: góc ABM< góc MBC
d/góc ABM=góc CEM, lại ở vị trí SLT nên AE//BC

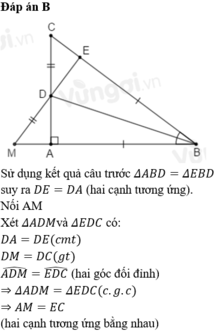
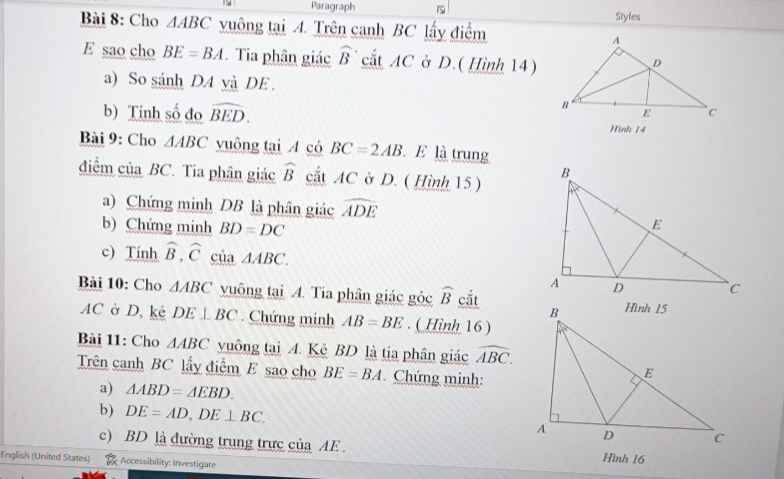
Bài 8:
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
b: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
Bài 9:
a: Ta có: BC=2AB
\(BC=2BE=2CE\)(E là trung điểm của BC)
Do đó: AB=BE=CE
Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>\(\widehat{BDA}=\widehat{BDE}\)
=>DB là phân giác của góc ADE
b: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Xét ΔDBC có
DE là đường cao
DE là đường trung tuyến
Do đó: ΔDBC cân tại D
=>DB=DC
c: Ta có: ΔBCD cân tại D
=>\(\widehat{DBC}=\widehat{DCB}\)
mà \(\widehat{DBC}=\dfrac{1}{2}\cdot\widehat{ABC}\)
nên \(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}\)
Ta có;ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\dfrac{1}{2}\cdot\widehat{ABC}+\widehat{ABC}=90^0\)
=>\(\dfrac{3}{2}\cdot\widehat{ABC}=90^0\)
=>\(\widehat{ABC}=60^0\)
=>\(\widehat{ACB}=\dfrac{1}{2}\cdot60^0=30^0\)

1:
a: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD
b: AB<AC
=>góc B>góc C
góc ADB=góc C+góc CAD
góc ADC=góc B+góc BAD
mà góc C<góc B và góc CAD=góc BAD
nên góc ADB<góc ADC

a,Xét tam giác ABM và tam giác EBM có :
AB = BE (gt)
góc B1 =góc B2(gt)
BM:cạnh chung
Suy ra tam giác ABM = tam giác EBM(c-g-c)
b,Do tam giác ABM = tam giác EBM ( cm câu a)
Suy ra AM = EM ( cặp cạnh tương ứng )
c,Do tam giác ABM = tam giác EBM ( cm câu a)
Suy ra góc BAM = góc BEM ( cặp cạnh tương ứng )
Mà góc BAM = 90 độ
Suy ra góc BEM = 90 độ
Bài làm đúng 100% đó,chúc bạn học tốt nhé!^.<

a: AB<AC
=>góc C<góc B
b: Xét ΔBAM vuông tại A và ΔBEM vuông tại E có
BM chung
BA=BE
=>ΔBAM=ΔBEM
c: Xét ΔBNC có
NE,CA là đường cao
NE cắt CA tại M
=>M là trực tâm
=>BM vuông góc CN