Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C F E D M N K
Ta có: EF // BD (gt)
BF // ED (gt)
Suy ra EF = BD; BF = DE (t/c đoạn chắn)
Trên AB lấy K sao cho AF = BK
\(\Delta AFE\) và \(\Delta KBD\) có:
AF = BK (cách vẽ)
AFE = KBD (đồng vị)
EF = BD (cmt)
Do đó, \(\Delta AFE=\Delta KBD\left(c.g.c\right)\)
=> AE = KD (2 cạnh t/ứ)
= BF = ED (theo gt AE = BF, theo cmt BF = ED)
Kẻ \(DM\perp AB;DN\perp AC\)
\(\Delta\) DMK vuông tại M và \(\Delta\) DNE vuông tại N có:
DK = DE (cmt)
MKD = NED (cùng đồng vị với FAE)
Do đó, \(\Delta DMK=\Delta DNE\) (cạnh huyền - góc nhọn)
=> DM = DN (2 cạnh t/ứ)
=> D cách đều AB và AC (đpcm)

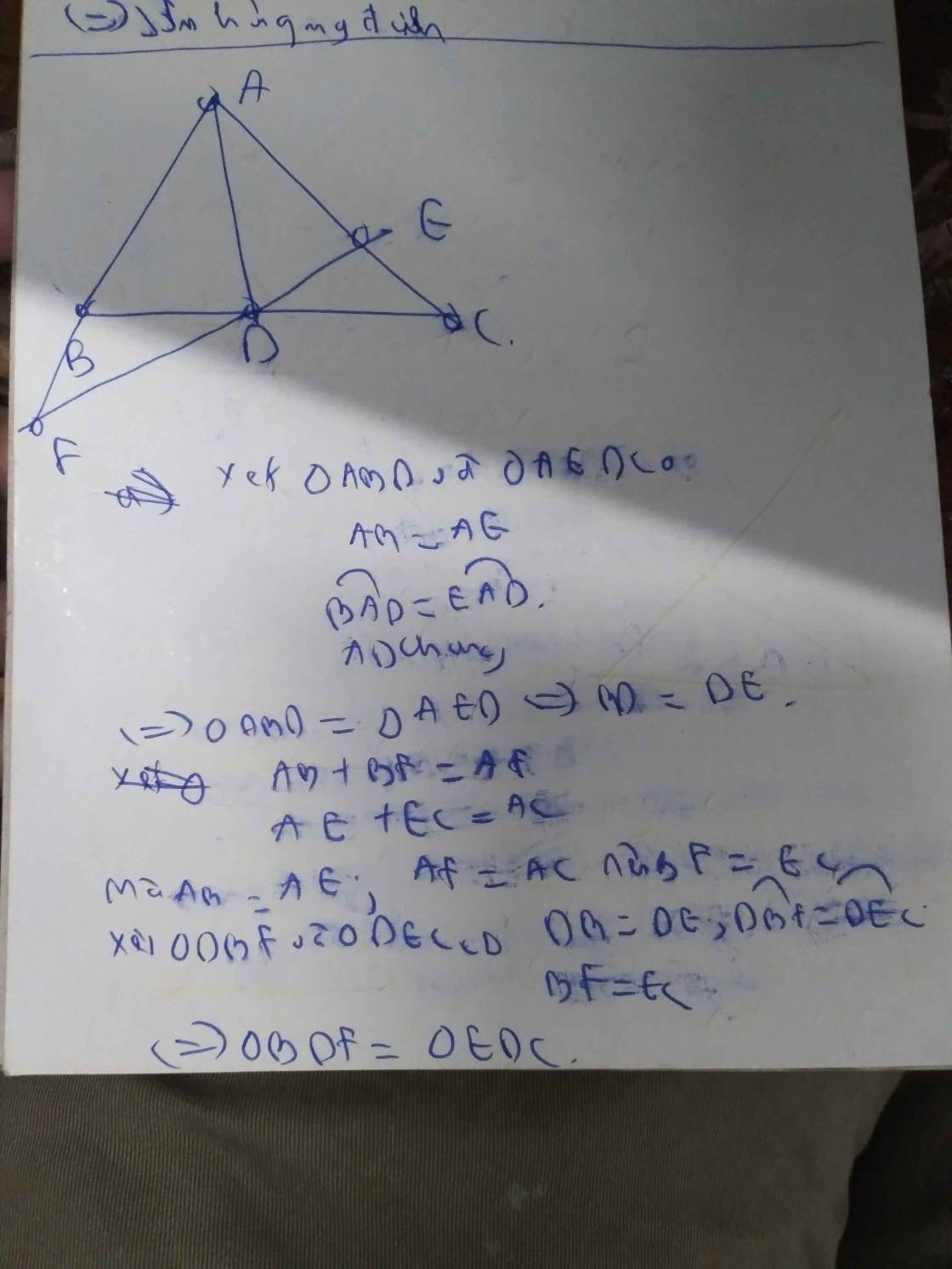
Cho tam giác ABC, AB<AC.Tia p/g của góc A cắt BC ở D, trên tia AC lấy điểm E sao cho AE=AB. Gọi tia M là giao điểm của AB va DE
Cmr: a) tam giác ABD=tam giacd AED
b) tam giacd DBM=tam giác DEC


a) Xét ΔABD và ΔAED có
\(\widehat{A_1}=\widehat{A_2}\)( tia phân giác AD của góc BAC)
AB=AE(GT)
AD chung
Nên ΔABD=ΔAED(c.g.c)
b)Ta có: AF=AC (GT)
=>ΔAFC vuông tại A
Mà AD là đường phân giác=>AD là đường cao
=>AD⊥FC
c)Ta có :ΔABD=ΔAED=>BD=DE(1), \(\widehat{B_1}=\widehat{E_1}\)
Mà \(\widehat{B_1}+\widehat{B_2}=180^o,\widehat{D_1}+\widehat{D_2}=180^o\)
=>\(\widehat{B_2}=\widehat{D_2}\)(2)
tA CÓ:AF=AC, AB=AE=>BF=EC(3)
Từ (1), (2), (3), ta có ΔBDF=ΔEDC(c.g.c)

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE
Xét ΔBDE và ΔEDC có
\(\widehat{BDF}=\widehat{EDC}\)
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
Do đó: ΔBDF=ΔEDC
A B C E D F
Ta sẽ nối điểm F với D
Ta có: EF//BC=>EF//BD(D\(\in\)BC)=>^EFD=^BDF(so le trong).
ED//AB=>ED//BF(F\(\in\)AB)=>^BFD=^EDF
Xét tam giác BFD và tam giác EDF:^EFD=^BDF; FD chung; ^BFD=^EDF=> Tam giác BFD = Tam giác EDF (g.c.g)
=>BF=ED(2 cạnh tương ứng). Mà AE=BF=>AE=ED(t/c bắc cầu)
Tam giác BFD=Tam giác EDF=>BD=FE=>^FBD=^FED(2góc tương ứng)
FE//BD=>^FBD=^AFE(đồng vị)
Xét tam giác BFD và tam giác FAE có: ^FBD=^AFE; BD=FE; ^FDB=^AEF=> Tam giác BFD=Tam giác FAE (g.c.g)
=>^BFD=^FAE=>FD//AE. Do FD//AE; ED//AF=>FD=AE; ED=AF(t/c đoạn chắn)
Mà DE=AE(cmt)=>DF=AF=AE=ED=>^FDE=^AED=90o
Xét tam giác FDE và tam giác AED: DE chung; ^FDE=^AED=90o; FD=AE=> Tam giác FDE=Tam giác AED(c.g.c)(1)
FD//EC=>^FDE=^CED(so le trg). FE//DC=>^FED=^CDE(so le trg)
Xét tam giác FED và tam giác CDE: ^FDE=^CED; DE chung; ^FED=^CDE=>Tam giác FED=Tam giác CDE(g.c.g)(2)
Từ (1) và (2)=> Tam giác AED=Tam giác CED=>DA=DC
=>Tam giác BFD=Tam giác DEC(g.c.g)=>DB=DA. mà DA=DC=> Điểm D cách đều AB và AC (đpcm)