Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em có thể suy ra những canh: HI = 2cm; IK = 4 cm;
.................................. góc : I = 40o

Ta có ΔABC = ΔHIK
Theo định nghĩa hai tam giác bằng nhau
HI = AB = 2cm
IK = BC = 4cm
góc I = góc B = 40º

Ta có ΔABC = ΔHIK
Theo định nghĩa hai tam giác bằng nhau
HI = AB = 2cm
IK = BC = 4cm
góc I = góc B = 40º
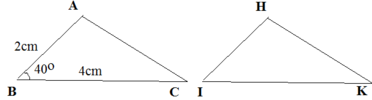
Cho tam giác ABC=HIK
Trong đó AB=2cm;góc B=40 độ, BC=4cm
Em có thể suy ra số đo của những cạnh góc nào


Do \(\Delta ABC=\Delta HIK\)
=> AB = HI = 2cm;
\(\widehat{B}=\widehat{I}=40^o\);
\(BC=IK=4cm\)

1 a,Ta có ∆ ABC= ∆ HIK, nên cạnh tương ứng với BC là cạnh IK
góc tương ứng với góc H là góc A.
ta có : ∆ ABC= ∆ HIK
Suy ra: AB=HI, AC=HK, BC=IK.
=
,
=
,
=
.
b,
∆ ABC= ∆HIK
Suy ra: AB=HI=2cm, BC=IK=6cm, =
=400
2.
Ta có ∆ABC= ∆ DEF
Suy ra: AB=DE=4cm, BC=EF=6cm, DF=AC=5cm.
Chu vi của tam giác ABC bằng: AB+BC+AC= 4+5+6=15 (cm)
Chu vi của tam giác DEF bằng: DE+EF+DF= 4+5+6=15 (cm

1) ΔABC = ΔHIK; AB =2cm; \(\widehat{B}\) = 40o; BC = 4cm
\(\Rightarrow\) AB = HI = 2cm
\(\widehat{B}\) = \(\widehat{I}\) = 40o
BC = IK = 4cm
Vậy ta có thể suy ra số đo của: cạnh HI , cạnh IK và \(\widehat{I}\)
2) ΔABC = ΔDEF ; AB = 4cm ; BC = 6cm ;
DF = 5cm
Ta có ΔABC = ΔDEF (gt) nên:
\(\Rightarrow\) DF = AC = 5cm ; AB = DE = 4cm ;
BC = EF = 6cm
Chu vi ΔABC là: AB + BC + AC
hay 4cm + 6cm+5cm = 11cm
Chu vi ΔDEF là: DE+ EF + DF
hay 4cm + 6cm+5cm = 11cm
Vậy chu vi: ΔABC = chu vi ΔDEF = 11cm

Vì \(\Delta ABC=\Delta HIK\)
\(\Rightarrow HI=AB=2cm\)( 2 cạnh tương ứng)
\(\widehat{I}=\widehat{B}=40^o\) ( 2 góc tương ứng)
\(IK=BC=4cm\)( 2 cạnh tương ứng)
\(\Delta ABC=\Delta HIK\)
\(\Rightarrow\left\{{}\begin{matrix}AB=HI;BC=IK;AC=HK\\\widehat{A}=\widehat{H};\widehat{B}=\widehat{I};\widehat{C}=\widehat{K}\end{matrix}\right.\)
như vậy ta có thể suy ra được:
\(HI=2cm;IK=40cm;\widehat{I}=40^0\)