Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

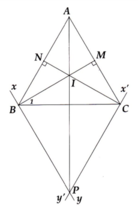
A B C I N M 1 2 1 2 1 2
Ta có: BI là phân giác \(\widehat{ABC}\Rightarrow\widehat{B_1}=\widehat{B_2}\)
CI là phân giác \(\widehat{ACB}\Rightarrow\widehat{C_1}=\widehat{C_2}\)
\(MN//BC\Rightarrow\widehat{I_1}=\widehat{B_2}\),\(\widehat{I_2}=\widehat{C_2}\)
+) Vì \(\widehat{B_1}=\widehat{B_2}\);\(\widehat{I_1}=\widehat{B_2}\)
\(\Rightarrow\widehat{B_1}=\widehat{I_1}\Rightarrow\Delta MBI\)cân tại M
\(\Rightarrow MB=MI\)
+) Vì \(\widehat{C_1}=\widehat{C_2}\);\(\widehat{I_1}=\widehat{C_2}\)
\(\Rightarrow\widehat{C_1}=\widehat{I_2}\Rightarrow\Delta NCI\)Cân tại N
\(\Rightarrow NC=NI\)
Ta có: \(MN=MI+NI\)
mà \(MB=MI\);\(NC=NI\)
\(\Rightarrow MN=MB+NC\left(đpcm\right)\)
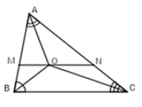


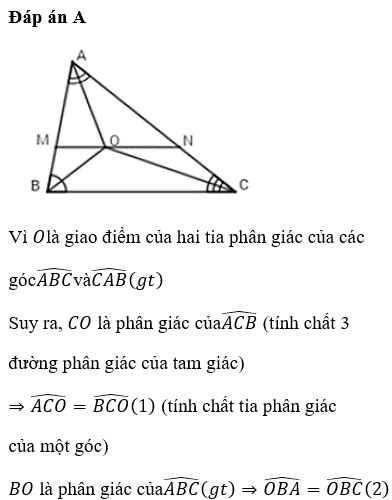


Vì OM//BC nên \(\widehat{MOB}=\widehat{MBO}\)
Ví ON//BC nên\(\widehat{ONC}=\widehat{OCN}\)
Xét \(\Delta BOM\)có \(\widehat{MOB}=\widehat{MBO}\)=> \(\Delta BOM\)cân (t/c)=> MB=MO
Xét \(\Delta OCN\)có \(\widehat{ONC}=\widehat{OCN}\)=> \(\Delta OCN\)cân (t/c)=> ON=NC
Ta lại có MO+ON=MN
=> BM+CN=MN (đpcm)
Vì OM // BC nên \(\widehat{MOB}\)= \(\widehat{MBO}\)
Vì ON // BC nên \(\widehat{ONC}\)= \(\widehat{OCN}\)
Xét \(\Delta BOM\)có \(\widehat{MOB}\)= \(\widehat{MBO}\)=> \(\Delta BOM\)cân (t/c) => MB = MO
Xét \(\Delta OCN\)có \(\widehat{ONC}\)= \(\widehat{OCN}\)=> \(\Delta OCN\)cân (t/c) => ON = NC
Ta có MO + ON = MN
=> BM + CN = MN ( đpcm )