K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 9 2023
Ta thấy \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{CM}\)
Như vậy, điểm M chính là đỉnh thứ tư của hình bình hành ABCM.
AH
Akai Haruma
Giáo viên
14 tháng 8 2021
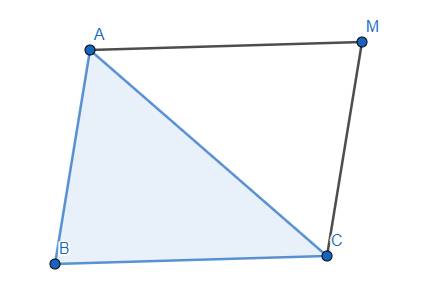
Lời giải:
a.
\(|\overrightarrow{MC}|=|\overrightarrow{MA}-\overrightarrow{MB}|=|\overrightarrow{BA|}\)
Tập hợp điểm $M$ thuộc đường tròn tâm $C$ đường bán kính $AB$
b. Gọi $I$ là trung điểm $AB$. Khi đó:
\(|\overrightarrow{MA}+\overrightarrow{MB}|=|\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}|\)
\(=|2\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{IB}|=|2\overrightarrow{MI}|=0\)
\(\Leftrightarrow |\overrightarrow{MI}|=0\Leftrightarrow M\equiv I\)
Vậy điểm $M$ là trung điểm của $AB$
AH
Akai Haruma
Giáo viên
14 tháng 8 2021
c.
Trên tia đối của tia $CA$ lấy $K$ sao cho $KC=\frac{1}{3}CA$
\(|\overrightarrow{MA}|=2|\overrightarrow{MC}|\Leftrightarrow |\overrightarrow{MK}+\overrightarrow{KA}|=2|\overrightarrow{MK}+\overrightarrow{KC}|\)
\(\Leftrightarrow |\overrightarrow{MK}+4\overrightarrow{KC}|=|2\overrightarrow{MK}+2\overrightarrow{KC}|\)
\(\Leftrightarrow (\overrightarrow{MK}+4\overrightarrow{KC})^2=(2\overrightarrow{MK}+2\overrightarrow{KC})^2\)
\(\Leftrightarrow MK^2+16KC^2=4MK^2+4KC^2\)
\(\Leftrightarrow 12KC^2=3MK^2\Leftrightarrow MK=2KC=\frac{2}{3}AC\)
Vậy $M$ thuộc đường tròn tâm $K$ bán kính $\frac{2}{3}AC$
PQ
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
8 tháng 12 2021
(MA+MB)(MC-MB)=0 => MC-MB=0 => MB=MC
=> tg MBC cân tại M
Từ M dựng đường thẳng d vuông góc với BC => d là đường cao của tg cân MBC => d đồng thời là đường trung trực
=> Tập hợp các điểm M thoả mãn đk đề bài là đường thẳng d là đường trung trực của BC
NH
20 tháng 9 2023
\(\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}-\overrightarrow{MC}=-\overrightarrow{MB}\Leftrightarrow\overrightarrow{CA}=\overrightarrow{BM}\)
Vậy M là điểm sao cho tứ giác ACBM là hình bình hành.
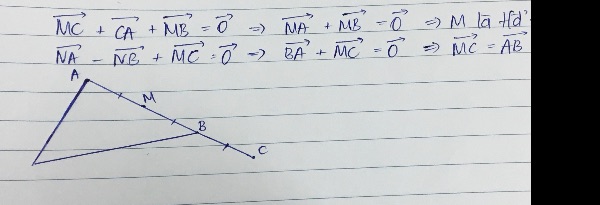
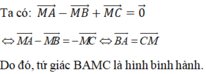
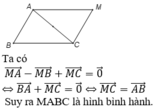
Đề có phải là: \(\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{0}\)
Gọi I là trung điểm AB
(Chèn điểm) \(\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}=\overrightarrow{MC}\)
\(\Leftrightarrow2\overrightarrow{MI}=\overrightarrow{MC}\)
Suy ra M nằm trên đường thẳng IC với I là trung điểm của MC