Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ah chăc câu này ghi nhầm đề nên ghi lại câu kia đung không. Thôi xem câu trên đi

A B C M H
Ta có : \(\left(sin\alpha+cos\alpha\right)^2=sin^2\alpha+cos^2\alpha+2sin\alpha.cos\alpha\) (1)
Lại có : \(sin^2\alpha=\frac{AB^2}{BC^2}\) ; \(cos^2\alpha=\frac{AC^2}{BC^2}\) \(\Rightarrow sin^2\alpha+cos^2\alpha=\frac{AB^2+AC^2}{BC^2}=\frac{BC^2}{BC^2}=1\) (2)
Kẻ đường cao AH (H thuộc BC)
Ta sẽ chứng minh \(sin\beta=2sin\alpha.cos\alpha\)
Xét tam giác vuông HMA có : \(sin\beta=\frac{AH}{AM}\)
Lại có \(AH=\frac{AB.AC}{BC}\) ; \(AM=\frac{BC}{2}\) \(\Rightarrow sin\beta=\frac{\frac{AB.AC}{BC}}{\frac{BC}{2}}=\frac{2AB.AC}{BC^2}=2.\frac{AB}{BC}.\frac{AC}{BC}=2sin\alpha.cos\alpha\)(3)
Từ (1) , (2) , (3) ta có điều phải chứng minh.

A B C M H
Kẻ đường cao AH ; Vì AB < AC => BH < HC=> H thuộc BM
Ta có: \(\sin\alpha=\frac{AB}{BC};\cos\alpha=\frac{AC}{BC};\sin\beta=\frac{AH}{AM}\)
=> \(\left(\sin\alpha+\cos\alpha\right)^2=\left(\frac{AB}{BC}+\frac{AC}{BC}\right)^2=\frac{AB^2}{BC^2}+\frac{AC^2}{BC^2}+\frac{2AB.AC}{BC^2}=1+\frac{2AB.AC}{BC^2}\)
Mà theo hệ thức lượng: \(AB^2=BC.BH;AC^2=CB.CH\)
=> \(\frac{2AB.AC}{BC^2}=2.\frac{AB}{BC}.\frac{AC}{BC}=\frac{2BH.CH}{AB.AC}=\frac{2AH^2}{AB.AC}\)
Ta cần chứng minh: \(\frac{2AH^2}{AB.AC}=\frac{AH}{AM}\Leftrightarrow2AH.AM=AB.AC\Leftrightarrow AH.BC=AB.AC\)đúng
Vậy \(1+\frac{2AB.AC}{BC^2}=1+\frac{AH}{AM}\)
=> Có điều cần phải cm
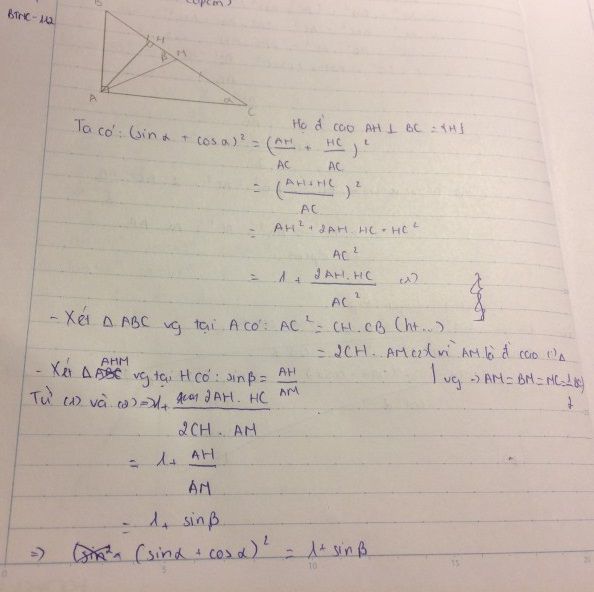
Ta co:
Vì tam ABC vuông tại A co D là trung điểm BC nên \(\widehat{MAC}=\widehat{MCA}=\frac{\widehat{AMB}}{2}\)
\(\Rightarrow\beta=2\alpha\)
Từ đây ta co:
\(cos^2\alpha-sin^2\alpha=cos\left(2\alpha\right)=cos\beta\)