Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AB=CD và AB//CD
b: Sửa đề: AB<AC
AB=CD
=>CD<AC
=>góc CAD<góc CDA
=>góc CAD<góc BAD
c: góc AMB=góc MAC+góc ACB
góc AMC=góc MAB+góc ABC
mà góc MAC<góc MAB và góc ACB<góc ABC
nên góc AMB<góc AMC

1: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: CD=AB
mà AB<AC
nên CD<AC
2: Ta có: \(\widehat{BAM}=\widehat{CDA}\)
mà \(\widehat{CDA}>\widehat{MAC}\left(AC>MC\right)\)
nên \(\widehat{BAM}>\widehat{CAM}\)

a) tam giác MAC = tam giác BAD theo trường hợp cạnh góc cạnh
Có: MC = MB (AM trung tuyến)
AMC = DMB (2 góc đối đỉnh)
MA = MD (theo giả thiết)
=> 2 tam giác bằng nhau theo trường hợp cạnh góc cạnh
b)
Tam giác ABC có góc A=90 độ
Suy ra: góc ACB+ góc CBA= 90 độ
Mà : góc ACB (hay góc ACM) = DBM (2 tam giác bằng nhau, chứng minh trên)
Suy ra: góc DBM + CBA = 90 độ
Hay DBA=90 độ

a)Xét hai tam giác ABM và DMC, ta có:
MA= MD(gt)
Góc ABM=CMD(đối đỉnh)
MB=MC(Vì AM là đường trung tuyến)
=> Tam giác ABM= Tam giác DMC(c.g.c)
b)Xét hai tam giác vuông AHB và EHB, ta có
AH=EH(gt)
AH: cạnh chung
=>tam giác AHB= tam giác EHM( 2 cạnh góc vuông)
=>AB=EM( 2 cạnh tương ứng)
=>tam giác ABE cân tại B
mình chỉ biết giải 2 câu thuj

Câu 1. bạn cm tam giác ABM bằng tg ECM suy ra góc BAM và CEM bằng nhau, AB bằng CE. mà AB nhỏ hơn AC nên CE nhỏ hơn AC. Xét tg ACE có CAE nhỏ hơn góc CEA. Suy ra góc CAE nhỏ hơn góc ABM.
Câu 2. cm tam giác ABD và EBD bằng nhau sra DE vuông góc với BC, AH//ED. Kéo dài DE Cắt AB tại K.cm 2 tam giác DEC và DAK bằng nhau. EC bằng AK. So sánh AK và EH bằng cách vẽ AM vuông góc với EK. Cm HE bằng AM. So sánh AM và AK trong tam giác vuông AMK có AM nhỏ hơn AK. Vậy HE nhỏ hơn EC. Chúc bạn học tốt.
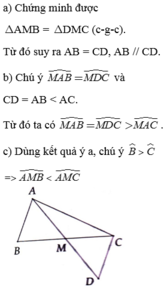
B A C M D 1 2
1)A)XÉT \(\Delta ABM\)VÀ\(\Delta DCM\)CÓ
\(BM=CM\left(GT\right)\)
\(\widehat{M_1}=\widehat{M_2}\left(Đ/Đ\right)\)
\(AM=DM\left(GT\right)\)
\(\Rightarrow\Delta ABM=\Delta DCM\left(C-G-C\right)\)
\(\Rightarrow AB=CD\)(HAI CẠNH TƯƠNG ỨNG)(1)
TA CÓ XÉT \(\Delta ABC\)VUÔNG TẠI B
\(\Rightarrow\widehat{B}>\widehat{C};\widehat{B}>\widehat{A}\)
VÌ\(\widehat{B}>\widehat{C}\)
\(\Rightarrow AB< AC\)QUAN HỆ GIỮA GÓC VÀ CẠNH ĐỐI DIỆN(2)
TỪ (1) VÀ (2) => \(AC>CD\)
B) CÂU B QUAN HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN
b) XÉT \(\Delta ADC\)
CÓ \(DC< AC\left(CMT\right)\)
\(\Rightarrow\widehat{ADC}>\widehat{DAC}\left(1\right)\)QUA HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN
MÀ \(\Delta ABM=\Delta DCM\left(CMT\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{MDC}\)
HAY\(\widehat{BAM}=\widehat{ADC}\left(2\right)\)
TỪ (1) VÀ (2) \(\Rightarrow\widehat{BMA}>\widehat{MAC}\)