Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

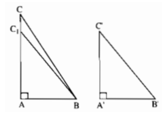
Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′. Ta có tam giác vuông ABC1 bằng tam giác vuông A'B'C', suy ra B′C′=BC1. Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1. Vì AC > AC1 nên BC > BC1. Suy ra BC > B'C'.

a: Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′.
Ta có ΔABC1=ΔA'B'C'
Suy ra B′C′=BC1
Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1.
Vì AC > AC1 nên BC > BC1.
Suy ra BC > B'C'.
b:
-Giả sử AC<A'C'.
Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).
Suy ra BC=B'C'.
Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.

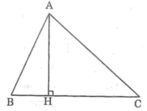
Vì điểm H nằm giữa B và C nên ta có: BH + HC = BC (1)
Lại có: AB > BH (đường xiên lớn hơn đường vuông góc)
AC > CH (đường xiên lớn hơn đường vuông góc)
Cộng từng vế ta có: AB + AC > BH + CH (2)
Từ (1) và (2) suy ra: AB + AC > BC

Theo giả thiết, tam giác ABC có độ dài cạnh BC là lớn nhất nên chân đường vuông góc kẻ từ A đến cạnh BC chắn chắn phải nằm giữa B và C.
Suy ra H nằm giữa B và C.
⇒ HB + HC = BC
+) Xét tam giác AHB vuông tại H ta có: HB < AB (1) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
+) Xét tam giác AHC vuông tại H ta có: HC < AC (2) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
Lấy (1) + (2) ta được:
HB + HC < AB + AC
Mà HB + HC = BC suy ra BC < AB + AC hay AB + AC > BC

a)Ta có:BD=BA(gt)
⇒ΔBAD cân tại B
⇒góc BAD=góc BDA
Trong ΔADH vuông tại H,có:
góc DAH+góc ADH=90 độ
Mà góc BAD+góc DAK=90 độ
⇒DAH+ADH=BAD+DAK
Mà góc ADH=góc BAD(cmt)
⇒Góc DAH=góc DAK
⇒AD là tia phân giác của góc HAC
b)Xét ΔADH và ΔADK,có:
góc H=góc K=90 độ
AD chung
góc DAH=góc DAK
⇒ΔADH=ΔADK(ch-gn)
⇒AH=AK(2 cạnh t/ứ)
c)Ta có:KC<DC(ΔKDC vuông tại K)
Mà KC=AC-AK
DC=BC-BD
⇒AC-AK<BC-BD
⇒ AC + BD < BC + AK
Mà BD=BA(gt)
⇒AK = AH (cmt)
⇒AB+AC<BC+AH
#Cừu

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)
Theo định lý Pytago, tam giác ABC ( Góc A=90 độ ) có:
\(BC^2=AB^2+AC^2\)
Mà AB, BC, AC > 0 nên BC2 > AB2, BC2 > AC2 hay BC > AB và AC suy ra BC lớn nhất